内点法
外观
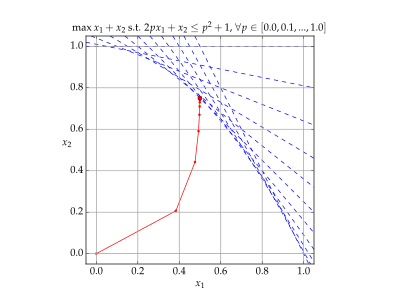
内点法(英語:Interior-point methods),也称为障碍法(英語:barrier methods),是解决线性和非线性凸优化问题的一类算法。
内点法由前苏联数学家伊·伊·迪金(I. I. Dikin)于1967年发现,并于20世纪80年代中期在美国重新发明。1984年纳伦德拉·卡玛卡(Narendra Karmarkar)开发了一种称为卡玛卡算法的线性规划方法,该算法在可证明的多项式时间内运行,并且在实践中也非常高效。它能够解决超出单纯形法能力的线性规划问题。与单纯形法不同,它通过遍历可行区域的内部来达到最佳解。该方法可以推广到基于用于编码凸集的自和谐障碍函数的凸规划。
通过转换为代码形式,任何凸优化问题都可以转化为最小化(或最大化)凸集上的线性函数[1]。安东尼·V·菲亚科、加斯·P·麦考密克等人在20世纪60年代初研究了使用屏障对可行集进行编码并设计屏障方法的想法。这些想法主要是针对一般非线性规划而开发的,但后来由于针对此类问题存在更具竞争力的方法(例如顺序二次规划)而被放弃。
尤里·涅斯捷羅夫和阿爾卡迪·內米羅夫斯基提出了一类特殊的障碍,可用于编码任何凸集。它们保证算法的迭代次数受解的维数和精度的多项式限制[2]。
尚博勒-波克算法于2011年推出,是一种通过最小化非平滑成本函数来有效解决凸优化问题的算法,涉及原对偶方法(primal-dualapproach)[3]。
卡玛卡的突破重振了内点方法和障碍问题的研究,表明可以创建一种以多项式复杂性为特征的线性规划算法,而且与单纯形法具有竞争力。哈奇延(Khachiyan)的椭球法已经是一种多项式时间算法,然而它太慢了因而没有实际意义[4]。
參考資料
[编辑]- ^ Boyd, Stephen; Vandenberghe, Lieven. Convex Optimization. Cambridge: Cambridge University Press. 2004: 143. ISBN 978-0-521-83378-3. MR 2061575.
- ^ Wright, Margaret H. The interior-point revolution in optimization: History, recent developments, and lasting consequences. Bulletin of the American Mathematical Society. 2004, 42: 39–57. MR 2115066. doi:10.1090/S0273-0979-04-01040-7
 .
.
- ^ Chambolle, Antonin; Pock, Thomas. A First-Order Primal-Dual Algorithm for Convex Problems with Applications to Imaging. Journal of Mathematical Imaging and Vision. 2011, 40 (1): 120–145. ISSN 0924-9907. doi:10.1007/s10851-010-0251-1 (英语).
- ^ Potra, Florian A.; Stephen J. Wright. Interior-point methods. Journal of Computational and Applied Mathematics. 2000, 124 (1–2): 281–302. doi:10.1016/S0377-0427(00)00433-7
 .
.
