截半大十二面體
 | |||
| 類別 | 星形均勻多面體 | ||
|---|---|---|---|
| 對偶多面體 | 内侧菱形三十面体 | ||
| 識別 | |||
| 名稱 | 截半大十二面體 | ||
| 參考索引 | U36, C45, W73 | ||
| 鮑爾斯縮寫 | Did | ||
| 數學表示法 | |||
| 威佐夫符號 | 2 | 5 5/2 2 | 5 5/3 2 | 5/2 5/4 2 | 5/3 5/4 | ||
| 性質 | |||
| 面 | 24 | ||
| 邊 | 60 | ||
| 頂點 | 30 | ||
| 歐拉特徵數 | F=24, E=60, V=30 (χ=-6) | ||
| 組成與佈局 | |||
| 頂點圖 | 5.5/2.5.5/2 | ||
| 頂點佈局 | 12{5}+12{5/2} | ||
| 對稱性 | |||
| 對稱群 | Ih, [5,3], *532 | ||
| 圖像 | |||
| |||
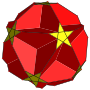
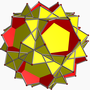
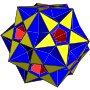
在幾何學中,截半大十二面體是一種星形均勻多面體,由12個正五邊形和12個正五角星組成,可以視為大十二面體或小星形十二面體截去所有頂點所產生的形狀。其對偶多面體為內側菱形三十面體。在抽象理論中,截半大十二面體可以視為五種無法良好具像化的抽象正多面體被部分具象化的結果。截半大十二面體由3個學者獨立發現,分別是埃德蒙·赫斯[1]、芭杜歐(Badoureau)[2]和皮奇(Pitsch)[3]。
性質
[编辑]截半大十二面體是一種非凸多面體,由24個面、60條邊和30個頂點組成[4],由於其具有點可遞的特性,因此屬於均勻非凸多面體之一,這種立體共有53種。在考克斯特、邁克爾·S·朗格·希金斯與傑弗里·查爾斯·珀西·米勒的書《均勻多面體》中,截半大十二面體被編號為U36,其也收錄於考克斯特的研究中,並且給予索引編號C45,1983年時,溫尼爾在他的書《多面體模型》中列出許多星形多面體模型,其中也收錄了此種形狀,並給予編號W73[5]。
面的組成
[编辑]截半大十二面體由12個正五邊形面和12個正五角星面組成。[6]每個頂點都是2個五邊形和2個五角星的公共頂點,在頂點圖中可以用(5,5/2,5,5/2)表示[7],其代表著面在頂點周圍是以五邊形面、五角星面、五邊形面、五角星面的方式交錯排佈。
威佐夫佈局
[编辑]截半大十二面體有四種威佐夫布局,其代表著四種史瓦茲三角形,其對應的威佐夫記號分別為: 2 | 5 5/2[8]、 2 | 5 5/3、 2 | 5/2 5/4[註 1]以及2 | 5/3 5/4。其雖然在威佐夫記號以不同方式表達,但實際上皆是代表相同的多面體。同理,截半大十二面體在施萊夫利符號中也可以用四種不同的方式表達,他們分別記為: t1{5/2,5}[11]、 t1{5/3,5}、 t1{5/2,5/4}以及t1{5/3,5/4}[12]。在考克斯特記號中,其同樣也存在四種形式,分別為:![]()
![]()
![]()
![]()
![]()
![]()
![]() 、
、 ![]()
![]()
![]()
![]()
![]()
![]()
![]() 、
、 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 以及
以及![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 。
。
展開圖
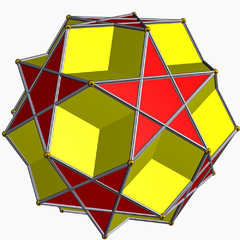
[编辑]截半大十二面體是一種星形多面體,同時,也能找到對應外觀相同的簡單多面體[註 2],其可以透過下列兩種形狀拼接而成:
其中需要12個五角星和20個三個菱形的組合[13]。由於這種結構使用了5個菱形來代替原有星形多面體的正五邊形面,因此組合出來的形狀部會包含原本就隱沒於截半大十二面體中的部分。[14]在這種結構下的截半大十二面體共由12個五角星面和60個菱形組成,且具有72個面、120條邊和90個頂點[15]。
用途
[编辑]相關多面體
[编辑]截半大十二面體的凸包為截半二十面体。其與兩種立體共用相同的邊布局,分別為小十二面半二十面体與大十二面半二十面体,其中小十二面半二十面体與截半大十二面體有相同的五角星面,而大十二面半二十面体則是正五邊形面與截半大十二面體的正五邊形面相同。[17]
 截半大十二面體 |
 小十二面半二十面体 |
 大十二面半二十面体 |
 截半二十面体 (凸包) |

截半大十二面體可以由小星形十二面體透過截半變換構造而成:
 小星形十二面體 |
 較淺的截角小星形十二面體 |
 均勻截角小星形十二面體 |
 截半小星形十二面體 |
截半大十二面體也可以由大十二面體透過截半變換構造而成[6]。隨著截角深度不斷加深,最終會變成對偶多面體[18]。而對大十二面體或小星形十二面體而言,截半大十二面體為其截角序列的中間點。[19]
| 名稱 | 小星形十二面體 | 截角小星形十二面體 | 截半大十二面體 | 截角大十二面體 | 大十二面體 |
|---|---|---|---|---|---|
| 考克斯特符號 | |||||
| 圖像 | 
|

|

|

|

|
拓樸正多面體
[编辑]由於截半大十二面體的五角星形面可經由拓樸變形變為五邊形面,因此,這種形狀在拓樸中相當於四階五邊形鑲嵌的商空間。[6][20]下圖中的紅色與黃色的五邊形分別代表拓樸形變前的五角星和正五邊形。
| 類別 | 抽象正多面體 |
|---|---|
| 對偶多面體 | 五階四邊形三十面體 |
| 數學表示法 | |
| 施萊夫利符號 | {5,4}6 |
| 性質 | |
| 面 | 24 |
| 邊 | 60 |
| 頂點 | 30 |
| 歐拉特徵數 | F=24, E=60, V=30 (χ=-6) |
| 虧格 | 4 |
| 組成與佈局 | |
| 面的種類 | 五邊形 |
| 對稱性 | |
| 對稱群 | S5, 120元素 |
此外,截半大十二面體也是一種不存在良好具像化實例的抽象正多面體的部分具像化實例之一[21][22]。在考克斯特於1977年出版的著作《正多胞形》中列出了五種不存在良好具像化實例的抽象正多面體。後來在1987年耶爾格·邁克爾·威利的論文又再次的確定了共存在五種有這種性質的抽象正多面體。[23]這種抽象多面體具有C2×S5對稱性,但只能具像化出一半的對稱性,即C2×A5或二十面體群對稱性。[24][25][26]
截半大十二面體在拓樸學上由24個五邊形組成,且每個頂點都是4個五邊形的公共頂點,因此在拓樸學上滿足抽象正多面體的定義。[24][25][26]然而這種抽象面體若是具象化為截半大十二面體則僅能具象化一半的對稱性。這種抽象正多面體可以對應到虧格為4的四階五邊形正則地區圖(施萊夫利符號:{5,4}6)[27],對應的皮特里多邊形為六邊形[27]。
| 多面體 |  內側菱形三十面體 |
 截半大十二面體 |
 內側三角六邊形二十面體 |
 雙三斜十二面體 |
 凹五角錐十二面體 |
|---|---|---|---|---|---|
| 種類 | {4,5}6 | {5,4}6 | {6,5}4 | {5,6}4 | {6,6}6 |
| 頂點圖 | {5}, {5/2} |
(5.5/2)2
|
{5}, {5/2} |
(5.5/3)3
|

|
| 面 | 30個菱形 |
12個五邊形 12個五角星 |
20個六邊形
|
12個五邊形 12個五角星 |
20個六邊形
|
| 鑲嵌 |  {4, 5} |
 {5, 4} |
 {6, 5} |
 {5, 6} |
 {6, 6} |
| χ | −6 | −6 | −16 | −16 | −20 |
參見
[编辑]註釋
[编辑]參考文獻
[编辑]- ^ Hess, Edmund, Vier archimedeische Polyeder höherer Art, Cassel. Th. Kay, 1878, JFM 10.0346.03
- ^ Badoureau, Mémoire sur les figures isoscèles, journal de l´École Polytechnique, 1881, 49: 47–172
- ^ Pitsch, Über halbreguläre Sternpolyheder, Zeitschrift für das Realschulwesen, 1882, 7, JFM 14.0448.01
- ^ Roman E. Maeder. 36: dodecadodecahedron. mathconsult.ch. [2019-09-26]. (原始内容存档于2019-03-18).
- ^ Wenninger, Magnus. Polyhedron Models. Cambridge University Press. 1974. ISBN 0-521-09859-9.
- ^ 6.0 6.1 6.2 6.3 David A. Richter. The Dodecadodecahedron and the Golay Code. wmich.edu. [2013-05-23]. (原始内容存档于2018-10-18).
- ^ Augmenting the dodecadodecahedron. orchidpalms.com. [2019-10-24]. (原始内容存档于2016-03-06).
- ^ Zvi Har'El. Kaleido Data: Uniform Polyhedron #41. harel.org.il. [2019-10-24]. (原始内容存档于2009-01-07).
- ^ Coxeter, The Evolution of Coxeter-Dynkin diagrams, [Nieuw Archief voor Wiskunde 9 (1991) 233-248]
- ^ great dodecadodecahedron. bulatov.org. [2019-09-06]. (原始内容存档于2017-10-11).
- ^ Dodecadodecahedron. 國立清華大學. May 18, 2011.
- ^ Coxeter, Longuet-Higgins, Miller, Uniform polyhedra, Phil. Trans. 1954, 246 A, 401-50
- ^ Geometric Model by Dick Holl, a Student of A.Harry Wheeler, Dodecadodecahedron. americanhistory.si.edu. [2019-09-26]. (原始内容存档于2019-09-26).
- ^ Paper Dodecadodecahedron. polyhedra.net.
- ^ Dodecadodecahedron. polyhedr.com. [2019-10-24]. (原始内容存档于2019-09-26).
- ^ Kythe, D.K. and Kythe, P.K. Algebraic and Stochastic Coding Theory. CRC Press. 2017: pp.151-152. ISBN 9781351832458.
- ^ U. Mikloweit. Did-Facetings. polyedergarten.de. [2019-09-26]. (原始内容存档于2018-11-18).
- ^ N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- ^ Robert Webb. Dodecadodecahedron. software3d.com. [2019-09-26]. (原始内容存档于2019-09-26).
- ^ Coxeter, H. S. M., Chapter 10: Regular honeycombs in hyperbolic space (PDF), The Beauty of Geometry: Twelve Essays, Dover Publications, 1999 [2019-09-26], ISBN 0-486-40919-8, LCCN 99035678, (原始内容存档 (PDF)于2016-06-10), invited lecture, ICM, Amsterdam, 1954.
- ^ The Regular Polyhedra (of index two) (页面存档备份,存于互联网档案馆), David A. Richter
- ^ The Golay Code on the Dodecadodecahedron (页面存档备份,存于互联网档案馆), David A. Richter
- ^ Wills, Jörg Michael. The combinatorially regular polyhedra of index 2. aequationes mathematicae (Springer). 1987, 34 (2-3): 206––220.
- ^ 24.0 24.1 David A. Richter. The Regular Polyhedra (of index two). 西密西根大學. (原始内容存档于2016-03-04).
- ^ 25.0 25.1 Regular Polyhedra of Index Two, I (页面存档备份,存于互联网档案馆) Anthony M. Cutler, Egon Schulte, 2010
- ^ 26.0 26.1 Regular Polyhedra of Index Two, II (页面存档备份,存于互联网档案馆) Beitrage zur Algebra und Geometrie 52(2):357–387 · November 2010, Table 3, p.27
- ^ 27.0 27.1 S4:{5,4}. Regular Map database - map details, weddslist.com. [2021-10-16].