潘洛斯三角
外观
(重定向自潘洛斯三角形)

潘洛斯三角(英語:Penrose triangle),又稱彭羅斯三角,是不可能物體中的一種。最早是由瑞典藝術家奧斯卡·路透斯沃德在1934年製作。英國數學家羅傑·潘洛斯及其父親莱昂内尔·彭罗斯設計及推廣,並在1958年2月份的《英國心理學月刊》(British Journal of Psychology)中發表,稱之為「最純粹形式的不可能」。
潘洛斯三角看起來像是一個固體,由三個截面為正方形的長方體所構成,三個長方體組合成為一個三角形,但兩長方體之間的夾角似乎又是直角。上述的性質無法在任何一個正常三維空間的物體上實現。這種物件只能存在於一些特定的歐氏三維流形中[1]。

潘洛斯三角雖然是不可能的物體,但是確實存在有三維物體,若在特定的角度下觀看時,其看到的圖案和潘洛斯三角的二維圖案相同。潘洛斯三角可以指不可能的物體本身,也可以指其二維下的圖案。
荷蘭藝術家莫里茨·科内利斯·埃舍尔的版畫瀑布描繪了一個沿著二個拉長的潘洛斯三角邊上曲折行進的水道,水道結束時的高度比原來的高度高二層樓,水最後形成瀑布,也是二個潘洛斯三角的短邊,再由瀑布驅動水車旋轉。
建筑
[编辑]
其他潘洛斯多邊形
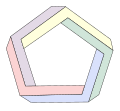
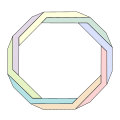
[编辑]可以依類似潘洛斯三角的方式創建其他的正多邊形,不過視覺上的衝擊效果不如潘洛斯三角,當邊數較多時,多邊形看起來只是像是由扭轉過的樑所構成。
參見
[编辑]參考資料
[编辑]- ^ Francis, George. A topological picturebook. Springer. 1988. ISBN 0-387-96426-6.,在書中有關潘洛斯三角的章節中,作者將以上觀察到的性質歸功於John Stillwell的成果
外部連結
[编辑]- An article about impossible triangle sculpture in Perth (页面存档备份,存于互联网档案馆)
- Escher for Real constructions
- Three-dimensional model of a Penrose triangle for SketchUp (页面存档备份,存于互联网档案馆)
- Build an impossible triangle
- Impossible sculptures by Francis Tabary (页面存档备份,存于互联网档案馆)
- A large Tribar in Austria/Europe (页面存档备份,存于互联网档案馆) At Camping Rosental Roz in Carinthia/Austria
- 「艾薛爾的『藝數』新視界」二部曲 (页面存档备份,存于互联网档案馆)