跳转到内容

科學模型

维基百科，自由的百科全书
科學模型的例子。 一個與大氣成分有關的化學和運輸過程示意圖。

科學模型 是科學研究中對一類研究方法的通稱，使用數學公式、電腦模擬或簡單的圖示來表示一個簡化的自然界，透過分析這個模型，以期能夠進一步了解科學，包括說明、驗證假說、或分析資料。依據不同需求，科學模型可以藉由概念模型幫助我們了解現象，操作模型給出操作型定義，數學模型幫助量化，以及用圖象模型將抽象概念視覺化。

科學模型是許多領域重要且不可分割的一部份，並且每種科學領域都有其特定的科學模型[1][2]。以約翰·馮·諾伊曼所說過的一段話為例[3]：

... 科學本身從來都不曾試圖去解釋自然現象，甚至是連詮釋自然現象的企圖都不曾有過，反而僅僅是建立模型。所謂的模型，就是——在數學意義上——去建構觀察到的自然現象之間的數學關係。而此模型令人信服的唯一理由，就僅僅是因為它確實有用——能夠描述足夠廣泛的自然現象。

近年來科學建模越發受重視[4]，例如在科學教育[5]、科學哲學、系統理論與視覺化 (電腦圖學)。科學建模也有其相關的科學方法、技術與形上學等議題。

目標和方法論

[编辑]
化學B-Z反應的電腦模擬。此反應可以用霍普夫分岔來描述。

科學模型依其在科學方法中佔據的位置，可以區分不同類型，包括概念模型和概念验证模型、預測模型、推理模型、以及統計模型等等。許多時候，做實驗是有困難的，所以用概念模型或預測模型代替實驗，避免物理、法律、時間、經費等限制[6]。模型是為了特定的目標而建，建模者根據自己的專業判斷，將不重要的細節排除、並將未驗證的資訊概括而入，最後達成目標。[7][8]

同一個現象有時會有許多解釋力一樣好的模型，然而模型描述的原理卻不同，這個現象叫作殊途同歸（equifinality）。例如人們接受新產品的比率往往呈一S型曲線，這可能是因為每個人對新科技的接受度不同，少數人特別開放，少數人特別保守，大多數人介於中間；另一個可能是新科技的傳播取決於現有使用者的人數和其競爭優勢，因此使用者太少或太多都會降低其接受率，兩個模型都會產生一樣的曲線[9]。如果模型之間在某些條件下會產生不同的預測，可能用實證研究判斷哪個模型正確。

另一方面，有些完全不同的現象背後的數學原理卻類似，可以用一樣的模型來描述，例如生物族群大小的振盪、心律不整、化學的B-Z反應、以及水龍頭滴水的速率都可以用霍普夫分岔來描述。在其著作《一種新科學》中，史蒂芬·沃爾夫勒姆主張大多數現象背後都有類似的簡單數學原理，因此推動科學進展的最有效方法是研究各種基本數學現象，例如細胞自動機。

概念模型

[编辑]
概念驗證模型的說明圖

概念模型是用模型來描述一個不容易用語言來描述的概念。概念模型可以用來說明一個科學理論或假說，或是驗證某個假說是否正確。好的概念模型可以清楚地說明系統運行的基本原理、排除不必要的資訊。如同實驗中的控制環境，科學模型排除多餘的變因，讓因果關係變得明顯。[10]

預測模型

[编辑]

預測模型將已知的數據套入理論中，計算出未知數。根據預測結果可以判斷模型的正確性、協助應對未來事件、比較不同決策的優劣等等。

統計模型

[编辑]
参见：現象學模型和概率模型

統計模型相當於假說和基本前提，代表的是產生數據的機制，將資料和統計模型一起放入資料分析後，可以判斷模型是否正確。但如果統計模型的某些前提不正確，可能會會推出錯誤結論。一般來說， 統計模型是一個機率密度函數，數據依據該函數產生。例如前提是各班級的學生成績是常態分佈，假說是且甲班成績低於乙班，依據學生t檢驗可以比較兩班的成績。常見的統計模型包括廣義線性模型等。

有些研究者會用許多反映不同假說的模型各自分析資料，然後用赤池信息量準則或貝葉斯信息準則等方法判斷哪一個模型「最好」，稱為模型選擇。然而最好的模型不見得最正確，例如在遇到對撞變因時，信息量準則會推薦錯誤的模型，因為在統計上控制對撞變因會讓偽關係更強，造成對撞變因被誤認為干擾變因。

推理模型

[编辑]

推理模型（inference model）比較不同的假說和實驗方法會產生什麼樣的數據，以了解科學研究過程中，科學家究竟可以從手邊的數據分析出哪些合理的推論。

本文屬於
研究系列
一部放置於一堆檔案材料附近的手提電腦
学术领域
研究设计（英语：Research design）
哲学学派（英语：List of schools of philosophy）
研究策略
方法论
方法
工具与软件
哲学主题

建模的過程

[编辑]

在確立目標和模型在科學研究中的功能後，操作定義和量化、挑選假設前提 ，然後依據這些前提建立模型：

  • 圖像模型：最簡單，不使用實際的公式推導，而是用圖象，例如經濟學的供需曲線。
  • 數學模型：需要數學能力
  • 電腦模擬：最複雜，需要寫程式的能力

首先必須明白問題的本質，才能根據研究目標將系統簡化成模型，用圖象、數學公式或程式碼來表示各種概念。判斷哪些核心部件必須保留、哪些可以簡化是建模的重要步驟。如果所有的細節都包含在內，模型和真實世界是一樣的，則沒有使用模型的意義。在許多研究領域有許多現有的模型框架可以使用，例如賽局理論、流行病SIR模型、流體力學公式、化學反應速率方程等等，許多時候研究者可以直接套用舊有的框架來研究新問題。然而，就算是研究一樣的問題，不同的研究者也可能因自己的偏好和對研究對象的理解不同而影響建模的判斷。

建模時的種種假設前提會限制模型的適用範圍。只有當前提正確時，模型才能保證正確，科學的進展往往始於用前提更廣的模型來取代舊有模型。例如狹義相對論預設慣性參考系，而廣義相對論進一步說明了這個前提的意義。

分析模型的方法有許多，包括計算模型的穩定狀態、求極值、描述變數之間的關係、用電腦模擬找趨勢等等。在變數的可能範圍很廣時，有時會在大範團快速掃描幾個數值套入模型後的結果，然後再依據這些結果挑選有興趣的範圍作細部的分析，這種手段稱為space mapping（英语：space mapping）。一般來說，分析模型後需要將結果可視化。

常用軟體

[编辑]

現代科學模型往往需要用到電腦，不管是計算複雜的算式、是將大量數據套入模型分析、作圖、或是電腦模擬皆然。在各領域，科學建模有許多不同模擬軟體和程式語言，也有人開發了協助建模的圖形介面。目前常見的包括Mathematica、Matlab、Python、Open Source Physics、Easy Java Simulations、 STELLA、Wolfram SystemModeler等等。

模型的好壞

[编辑]

怎樣才算是好的模型是科學哲學和科學史學者尚在研究的問題。常見的觀點是好的模型應該要有以下特質：[11]

  1. 漂亮，沒有專為特定目標而存在的修改（ad hoc modifications）
  2. 簡約，少有任意、可改動的變數（奧卡姆剃刀）
  3. 有解釋力，和現有的各種證據吻合
  4. 能產生精確的預測，未來有機會否證
  5. 可以提供重要的見解、指引未來的研究。

然而這些判準是主觀的，沒有固定的標準，而且符合這些特質的模型不見得比較正確[12]，例如愛因斯坦曾說：「所有的東西應該盡可能地簡單，但不能比這更簡單。」除此之外，歷史上發生的各種典範轉移是否都是如此換成更好的模型也有爭議，例如日心說的解釋力在當時並沒有比地心說更高[13]。

各領域的模型發展史

[编辑]

微積分和物理

[编辑]
主条目：物理模型

17世紀是微積分的發展時期，戈特弗里德·威廉·萊布尼茨和艾薩克·牛頓兩人幾乎同時使微積分觀念成熟，澄清微、積分之間的關係，使計算系統化，並且把微積分大規模使用到幾何與物理研究上。牛顿利用了微積分的技巧，由萬有引力及運動定律出發說明了他的宇宙體系，解决天体运动，流体旋转的表面，地球的扁率，摆线上重物的运动等问题[14]。

如今，純物理的模型大多為概念驗證模型，例如標準模型以及其他尚未確認的弦論、多重宇宙等。應用物理的模型則較多模擬和預測。

人口和族群動力模型

[编辑]

1798年馬爾薩斯提出人口的指數成長模型。

1925和1926年，洛特卡－沃爾泰拉方程，成為生態學以及演化生物學描述生物互動的基礎。之後Kermack–McKendrick theory（英语：Kermack–McKendrick theory）為流行病學的分室系統方法（英语：compartmental model）打下基礎。1945年，萊斯利矩陣（英语：Leslie matrix）將不同年齡的生殖和存活率列入考慮，用線性代數更詳盡地描述生物族群的成長。

機率和統計模型

[编辑]

1906年的馬可夫鏈描述離散狀態、離散時間的隨機轉換。

1908年和1909年的哈溫平衡描述不同基因型在族群中的基因頻率，是遺傳學的基礎。卡爾·皮爾森和法蘭西斯·高爾頓等人開始發展生物統計學，之後羅納德·費雪、休厄爾·賴特、JBS·霍爾丹等人計算生物基因或性狀在族群中的分佈，促生現代演化綜論，包括族群遺傳學、計量遺傳學等各種模型。因為基因頻率和機率的關係密不可分，許多模型描述的是隨機過程，例如描述遺傳漂變的賴特-費雪模型（英语：Wright-Fisher model）和Moran模型（英语：Moran process）。

供需模型

[编辑]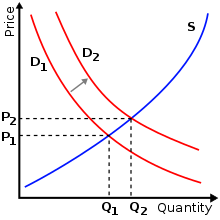
供給與需求的模型解釋了產品的數量和需求間的互動。圖中解釋從D1到D2的需求移動，會連帶地使得產品的供給數量和價格提高，如此一來才能達到新的均衡點。
主条目：经济学 § 歷史

供給和需求的概念早在中世紀一些穆斯林經濟學家即有[15]。在歐洲的學術界，1767年詹姆士·斯图亚特、1776年亞當·斯密、1817年李嘉圖都有使用[16]。1838年法國數學家古諾首先發展一個數學化的供需模型。

19世紀晚期邊際效用學派興起，這個學派以英國經濟學家傑文斯、奧地利經濟學家門格爾和法國經濟學家瓦爾拉斯爲首。他們理論的共同點是價格是由生產決策的邊際價格決定。這是自從亞當·斯密關於如何決定供給價格的思想以來一個非常重要的改變。1870年作者弗萊明·詹金（Fleeming Jenkin）首先在論文裏繪出第一條供給曲線和需求曲線[17]，包括使用比較靜態的辦法研究供給和需求在勞動市場的應用[18] 。這個模型後來被馬歇爾在其1890年的教科書著作《經濟學原理》（Principles of Economics）進一步發展及普及[16]。

賽局

[编辑]

对于博弈论的研究开始于1913年的恩斯特·策梅洛、後經埃米尔·博雷尔、冯·诺伊曼和奥斯卡·摩根斯坦，在1940年代系统化和形式化。随后约翰·福布斯·纳什利用不动点定理证明了均衡点的存在，为博弈论的一般化奠定了坚实的基础。纳什和约翰·C·海萨尼及萊因哈德·澤爾騰因为他们对博弈论的贡献而获得1994年的諾貝爾經濟學獎。罗伯特·J·奥曼、肯·宾摩尔、戴维·克瑞普斯及阿里尔·鲁宾斯坦也對博弈论做出重大貢獻。

1970年代，約翰·梅納德·史密斯（英语：John Maynard Smith）和喬治·普萊斯（英语：George R. Price）將賽局理論應用到生物學上，建立演化均衡策略（英语：evolutionary stable strategy）的概念。

電腦

[编辑]

電腦的發展對科學模型有重要的貢獻，許多本來過於困難或花時間的計算都因為電腦而得以進行。1940年代發展的蒙地卡羅方法用亂數來解決很多計算問題，例如和馬可夫鏈結合後處理貝氏統計模型。硬體的升級以及平行運算等技術則讓大數據得以發展。機器學習甚至讓模型的複雜度超過人類可以理解的範圍。

電腦的快速運算促成許多仰賴模擬的科學模型，例如強調個體差異的個體為本模擬為生態學作出重大貢獻。氣象預報模型則描述難以用有限的數學公式推算的複雜系統。透過模擬有機化學的各種機制，電腦模擬也用在找尋新藥物[19]以及晶片設計。

心理學

[编辑]

1971年，Schelling用個體為本模型說明為什麼即使人們沒有種族主義傾向，居住區域也可能發生種族隔離，是最早將科學模型用在心理學的例子之一[20]。現在，科學模型、質化研究、量化研究、訪問、和文本分析是心理學的五大研究方法[21]。

科學模型也廣泛應用在認知科學，例如用電腦模擬幾種不同的規則來判斷語句應如何發生閩南語連續變調，以研究語言學習的認知過程[22]。

參考資料

[编辑]
  1. ^ Cartwright, Nancy. 1983. How the Laws of Physics Lie （页面存档备份，存于互联网档案馆）. Oxford University Press
  2. ^ Hacking, Ian. 1983. Representing and Intervening. Introductory Topics in the Philosophy of Natural Science. Cambridge University Press
  3. ^ von Neumann, J. (1995), "Method in the physical sciences", in Bródy F., Vámos, T. (editors), The Neumann Compendium, World Scientific, p. 628; previously published in The Unity of Knowledge, edited by L. Leary (1955), pp. 157-164, and also in John von Neumann Collected Works, edited by A. Taub, Volume VI, pp. 491-498.
  4. ^ Frigg and Hartmann (2009) state: "Philosophers are acknowledging the importance of models with increasing attention and are probing the assorted roles that models play in scientific practice". Source: Frigg, Roman and Hartmann, Stephan, "Models in Science", The Stanford Encyclopedia of Philosophy (Summer 2009 Edition), Edward N. Zalta (ed.), (source （页面存档备份，存于互联网档案馆）)
  5. ^ Namdar, Bahadir; Shen, Ji. Modeling-Oriented Assessment in K-12 Science Education: A synthesis of research from 1980 to 2013 and new directions. International Journal of Science Education. 2015-02-18, 37 (7): 993–1023. ISSN 0950-0693. doi:10.1080/09500693.2015.1012185. 
  6. ^ Tolk, A. (2015). Learning something right from models that are wrong – Epistemology of Simulation. In Yilmaz, L. (Ed.) Concepts and Methodologies in Modeling and Simulation. Springer–Verlag. pp. 87–106
  7. ^ Oberkampf, W. L., DeLand, S. M., Rutherford, B. M., Diegert, K. V., & Alvin, K. F. (2002). Error and uncertainty in modeling and simulation. Reliability Engineering & System Safety 75(3): 333–57.
  8. ^ Ihrig, M. (2012). A New Research Architecture For The Simulation Era. In European Council on Modelling and Simulation. pp. 715–20).
  9. ^ Cavalli-Sforza, L. L., & Feldman, M. W. (1981). Cultural transmission and evolution: A quantitative approach (No. 16). Princeton University Press.
  10. ^ C.H. Kung, A. Solvberg, Activity Modeling and Behavior Modeling, In: T. Ollie, H. Sol, A. Verrjin-Stuart, Proceedings of the IFIP WG 8.1 working conference on comparative review of information systems design methodologies: improving the practice. North-Holland, Amsterdam (1986), pp. 145–71. Portal.acm.org. [2014-06-20]. 
  11. ^ Mark Colyvan. The Indispensability of Mathematics. Oxford University Press. 2001: 78–79 [2020-06-18]. ISBN 0195166612. （原始内容存档于2020-09-22）. 
  12. ^ Bird, Alexander. Edward N. Zalta , 编. §4.1 Methodological Incommensurability. The Stanford Encyclopedia of Philosophy (Spring 2013 Edition). Aug 11, 2011 [2020-06-18]. （原始内容存档于2014-02-25）. 
  13. ^ Thomas S Kuhn. The structure of scientific revolutions (PDF) 3rd. University of Chicago Press. 1966 [2020-06-18]. ISBN 0226458083. （原始内容存档 (PDF)于2017-08-09）. 
  14. ^ Donald Allen. Calculus. （原始内容存档于2021-03-23） （英语）. 
  15. ^ Hosseini, Hamid S. Contributions of Medieval Muslim Scholars to the History of Economics and their Impact: A Refutation of the Schumpeterian Great Gap. Biddle, Jeff E.; Davis, Jon B.; Samuels, Warren J. (编). A Companion to the History of Economic Thought. Malden, MA: Blackwell. 2003: 28–45 [28 & 38]. ISBN 0631225730. doi:10.1002/9780470999059.ch3. 
  16. ^ 16.0 16.1 Thomas M. Humphrey, 1992. "Marshallian Cross Diagrams and Their Uses before Alfred Marshall," Economic Review, Mar/Apr, Federal Reserve Bank of Richmond, pp. 3-23. （页面存档备份，存于互联网档案馆）
  17. ^ A.D. Brownlie and M. F. Lloyd Prichard, 1963. "Professor Fleeming Jenkin, 1833-1885 Pioneer in Engineering and Political Economy," Oxford Economic Papers, NS, 15(3), p. 211.
  18. ^ Fleeming Jenkin, 1870. "The Graphical Representation of the Laws of Supply and Demand, and their Application to Labour," in Alexander Grant, ed., Recess Studies, Edinburgh. ch. VI, pp. 151-85. Edinburgh. Scroll to chapter link. （页面存档备份，存于互联网档案馆）
  19. ^ Atanasov, AG; Waltenberger, B; Pferschy-Wenzig, EM; Linder, T; Wawrosch, C; Uhrin, P; Temml, V; Wang, L; Schwaiger, S; Heiss, EH; Rollinger, JM; Schuster, D; Breuss, JM; Bochkov, V; Mihovilovic, MD; Kopp, B; Bauer, R; Dirsch, VM; Stuppner, H. Discovery and resupply of pharmacologically active plant-derived natural products: A review. Biotechnol Adv. 2015, 33 (8): 1582–614. PMC 4748402 可免费查阅. PMID 26281720. doi:10.1016/j.biotechadv.2015.08.001. 
  20. ^ Schelling, T. C. (1971). Dynamic models of segregation. Journal of mathematical sociology, 1(2), 143-186.
  21. ^ Mesly, Olivier (2015). Creating Models in Psychological Research. United States: Springer Psychology: 126 pages. ISBN 978-3-319-15752-8
  22. ^ Chang, Y. C. A Knowledge Representation Method to Implement A Taiwanese Tone Group Parser [In Chinese]. International Journal of Computational Linguistics & Chinese Language Processing. 2017, 22 (212): 73–86. 
检索自“https://zh1.bitforum.be.eu.org/w/index.php?title=科學模型&oldid=80033810”