AVL树
| AVL樹 | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 类型 | 樹 | ||||||||||||||||||||
| 发明时间 | 1962年 | ||||||||||||||||||||
| 发明者 | 格奥尔吉·阿杰尔松-韦利斯基 葉夫根尼·蘭迪斯 | ||||||||||||||||||||
| 用大O符号表示的时间复杂度 | |||||||||||||||||||||
| |||||||||||||||||||||

AVL树(英語:AVL tree)是计算机科学中最早被发明的自平衡二叉查找树。在AVL树中,任一节点对应的两棵子树的最大高度差为1,因此它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下的時間複雜度都是 。增加和删除元素的操作则可能需要藉由一次或多次树旋转,以实现树的重新平衡。AVL树得名于它的发明者格奥尔吉·阿杰尔松-韦利斯基和葉夫根尼·蘭迪斯,他们在1962年的论文《An algorithm for the organization of information》中公开了这一数据结构。
节点的平衡因子是它的左子树的高度减去它的右子树的高度(有時相反)。带有平衡因子1、0或 -1的节点被认为是平衡的。带有平衡因子 -2或2的节点被认为是不平衡的,并需要重新平衡这个树。平衡因子可以直接存储在每个节点中,或从可能存储在节点中的子树高度计算出来。
操作
[编辑]
AVL树的基本操作一般涉及运作同在不平衡的二叉查找树所运作的同样的算法。但是要进行预先或随后做一次或多次所谓的"AVL旋转"。
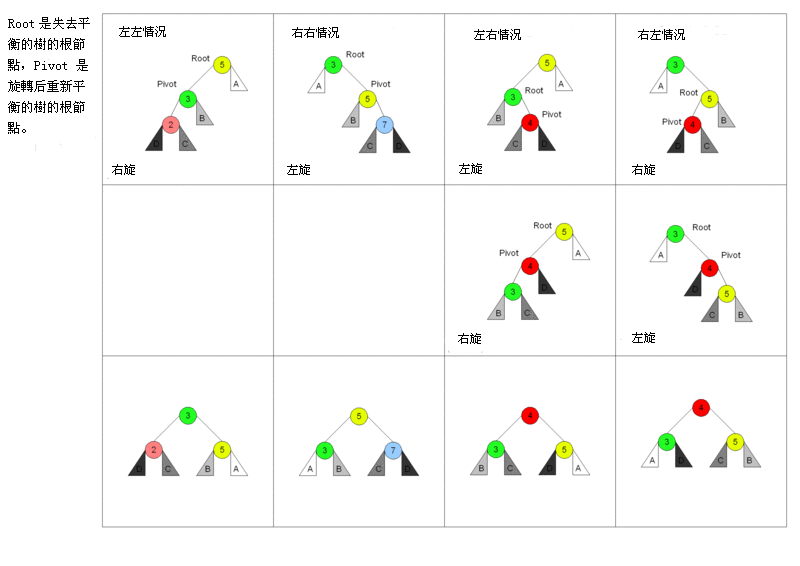
以下图表以四列表示四种情况,每行表示在该种情况下要进行的操作。在左左和右右的情况下,只需要进行一次旋转操作;在左右和右左的情况下,需要进行两次旋转操作。
删除
[编辑]从AVL树中删除,可以通过把要删除的节点向下旋转成一个葉子節點,接着直接移除这个叶子节点来完成。因为在旋转成葉子節點期间最多有log n个节点被旋转,而每次AVL旋转耗费固定的时间,所以删除处理在整体上耗费O(log n) 时间。
搜尋
[编辑]可以像普通二叉查找树一样的进行,所以耗费O(log n)时间,因为AVL树总是保持平衡的。不需要特殊的准备,树的结构不会由于查找而改变。(这是与伸展樹搜尋相对立的,它会因为搜尋而变更树结构。)
实现描述
[编辑]假設平衡因子是左子樹的高度減去右子樹的高度所得到的值,又假设由于在二叉排序树上插入节点而失去平衡的最小子树根节点的指针为a(即a是离插入点最近,且平衡因子绝对值超过1的祖先节点),则失去平衡后进行的规律可归纳为下列四种情况:
- 单向右旋平衡处理LL:由于在*a的左子树根节点的左子树上插入节点,*a的平衡因子由1增至2,致使以*a为根的子树失去平衡,则需进行一次右旋转操作;
- 单向左旋平衡处理RR:由于在*a的右子树根节点的右子树上插入节点,*a的平衡因子由-1变为-2,致使以*a为根的子树失去平衡,则需进行一次左旋转操作;
- 双向旋转(先左后右)平衡处理LR:由于在*a的左子树根节点的右子树上插入节点,*a的平衡因子由1增至2,致使以*a为根的子树失去平衡,则需进行两次旋转(先左旋后右旋)操作。
- 双向旋转(先右后左)平衡处理RL:由于在*a的右子树根节点的左子树上插入节点,*a的平衡因子由-1变为-2,致使以*a为根的子树失去平衡,则需进行两次旋转(先右旋后左旋)操作。
在平衡的二叉排序树BBST (Balancing Binary Search Tree)上插入一个新的数据元素e的递归算法可描述如下:
- 若BBST为空树,则插入一个数据元素为e的新节点作为BBST的根节点,树的深度增1;
- 若e的关键字和BBST的根节点的关键字相等,则不进行;
- 若e的关键字小于BBST的根节点的关键字,而且在BBST的左子树中不存在和e有相同关键字的节点,则将e插入在BBST的左子树上,并且当插入之后的左子树深度增加(+1)时,分别就下列不同情况处理之:
- BBST的根节点的平衡因子为-1(右子树的深度大于左子树的深度):则将根节点的平衡因子更改为0,BBST的深度不变;
- BBST的根节点的平衡因子为0(左、右子树的深度相等):则将根节点的平衡因子更改为1,BBST的深度增1;
- BBST的根节点的平衡因子为1(左子树的深度大于右子树的深度):则若BBST的左子树根节点的平衡因子为1:则需进行单向右旋平衡处理,并且在右旋处理之后,将根节点和其右子树根节点的平衡因子更改为0,树的深度不变;
- 若e的关键字大于BBST的根节点的关键字,而且在BBST的右子树中不存在和e有相同关键字的节点,则将e插入在BBST的右子树上,并且当插入之后的右子树深度增加(+1)时,分别就不同情况处理之。
AVL树的调平(Erlang的实现)
balance(null) -> null;
balance({null, _, null}=Tree) -> Tree;
balance({Left, Value, Right}=Tree) ->
Diff = count(Left)-count(Right),
if (Diff < 2) and (Diff > -2) -> {balance(Left), Value, balance(Right)};
(Diff > 1) -> balance(rotate_right(Tree));
(Diff< -1) -> balance(rotate_left(Tree));
true -> exit('This is impossible!')
end.
rotate_right({Left, Value, Right}) ->
merge_max(Left, {null, Value, Right}).
rotate_left({Left, Value, Right}) ->
merge_min(Right, {Left, Value, null}).
merge_min({null, Value, Right}, Tree2) ->
{Tree2, Value, Right};
merge_min({Left, _, _}, Tree2) ->
merge_min(Left, Tree2).
merge_max({Left , Value, null}, Tree2) ->
{Left, Value, Tree2};
merge_max({_, _, Right}, Tree2) ->
merge_max(Right, Tree2).
AVL節點數計算
[编辑]高度為h的AVL樹,總節點數N最多;
最少節點數如以斐波那契數列可以用數學歸納法證明:
= - 1 (是斐波那契数列的第h+2项,根据斐波那契多项式得来)。
即:
= 0 (表示AVL Tree高度為0的節點總數)
= 1 (表示AVL Tree高度為1的節點總數)
= 2 (表示AVL Tree高度為2的節點總數)
= + + 1 (表示AVL Tree高度為h的節點總數)
換句話說,當節點數為N時,高度h最多為。
参见
[编辑]引用
[编辑]- G. Adelson-Velskii and E.M. Landis, "An algorithm for the organization of information." Doklady Akademii Nauk SSSR, 146:263–266, 1962(Russian). English translation by Myron J. Ricci in Soviet Math. Doklady, 3:1259–1263, 1962.
外部链接
[编辑]- Description from the Dictionary of Algorithms and Data Structures(页面存档备份,存于互联网档案馆)
- AVL Tree Traversal(页面存档备份,存于互联网档案馆)
- Linked AVL tree
- C++ AVL Tree Template and C AVL TREE "Generic Package" by Walt Karas
- A Visual Basic AVL Tree Container Class(页面存档备份,存于互联网档案馆) by Jim Harris
- AVL Trees: Tutorial and C++ Implementation(页面存档备份,存于互联网档案馆) by Brad Appleton
- Ulm's Oberon Library: AVLTrees(页面存档备份,存于互联网档案馆)
- The AVL TREE Data Type
- CNAVLTree Class Reference[永久失效連結]
- GNU libavl(页面存档备份,存于互联网档案馆)
- AVL-trees - balanced binary trees by Alex Konshin
- Simulation of AVL Trees
- AVL tree applet(页面存档备份,存于互联网档案馆)
- Simulation of AVL Trees (DYNAMIC)
- AVL, Splay and Red/Black Applet
- Data Structures and Algorithm Analysis in C (2nd edition) (页面存档备份,存于互联网档案馆)