User:AnthonyDonlon/wip/多重对数函数

在数学中，多重对数函数（英语：polylogarithm，也称为 Jonquière 函数）是一类有着阶数 s 和参数 z 的特殊函数Li_s(z)。只有当 s 为特殊值时，多重对数函数才退化为初等函数（如自然对数或有理函数）。在量子统计中，多重对数函数可作为费米–狄拉克分布和玻色–爱因斯坦分布的积分的闭式解，也因此被称为费米–狄拉克积分或玻色–爱因斯坦积分。在量子电动力学中，正整数阶的多重对数函数出现的计算程序表示高阶费曼图。

多重对数函数与赫尔维茨ζ函数等价，二者可以相互表示，且都是勒奇超越函数的特例。多重对数函数不应与多对数函数或对数积分混淆，尽管它们有相似的记号，但后者只有一个变量。

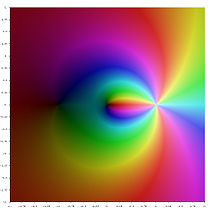
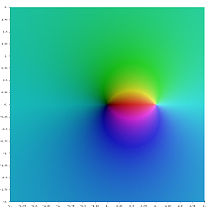
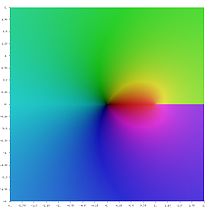
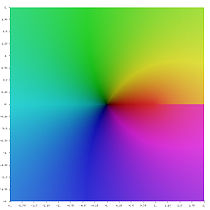
• 复平面中不同的多重对数函数
• 
  Li₋₃(z)
• 
  Li₋₂(z)
• 
  Li₋₁(z)
• 
  Li₀(z)
• 
  Li₁(z)
• 
  Li₂(z)
• 
  Li₃(z)

多重对数函数由关于 z 的幂级数定义，这个级数也是关于 s 的狄利克雷级数：

$\operatorname {Li} _{s}(z)=\sum _{k=1}^{\infty }{z^{k} \over k^{s}}=z+{z^{2} \over 2^{s}}+{z^{3} \over 3^{s}}+\cdots$

在阶数 s 为任意复数且复数参数 |z| < 1 时，这个定义有效。但这个式子也可被解析延拓至 |z| ≥ 1 上。在s = 1 的特殊情况下，多重对数函数将与自然对数有关，Li₁(z) = -ln(1-z)，而在特殊情况 s = 2 和 s = 3 时，多重对数函数则变为二重对数函数（也称为斯盆司函数）和三重对数函数。双重对数函数的名称来自于它能被定义为它自身的积分这一性质：

$\operatorname {Li} _{s+1}(z)=\int _{0}^{z}{\frac {\operatorname {Li} _{s}(t)}{t}}dt$

这样，二重对数函数(s = 2)就是与对数有关的函数的积分，依此类推。对于非正的整数阶数s，多重对数函数是一个有理函数。

属性

在多重对数函数阶的阶数$s$是一个整数时，$s$可由$n$表示（或$-n$，当其为负数时）。通常，可以定义$\mu =\ln(z)$为复数对数$\operatorname {Ln} (z)$的主支以便于使用，这样一来就有$-\pi <\operatorname {Im} (\mu )\leq \pi$。此外，所有指数都将被认定是单值的：$z^{s}=\exp(s\ln(z)).$

在不同的阶数$s$下，多重对数函数可能是多值的。$\operatorname {Li} _{s}(z)$的主支被认为是为了$|z|<1$根据上述系列定义，除在正实轴上切割成$z=1$至$\infty$以便将轴放置在$z$。就......而言$\mu$，这等于$-\pi <\operatorname {arg} (-\mu )\leq \pi$。多重对数函数的不连续性取决于$\mu$有时会令人困惑。

对于实的参数$\displaystyle z$，在当$\displaystyle z<1$时，实数阶$s$的多重对数函数的函数值也是实数。而当$z\geq 1$时，其虚部是(Wood 1992，§ 3):

$\operatorname {Im} \left(\operatorname {Li} _{s}(z)\right)=-{{\pi \mu ^{s-1}} \over {\Gamma (s)}}.$

越过边界，如果ε是一个无限小的正实数，那么：

$\operatorname {Im} \left(\operatorname {Li} _{s}(z+i\epsilon )\right)={\pi \mu ^{s-1}} \over {\Gamma (s)}.$

而者都可以从 Li_s(e^µ)在 µ = 0 处的级数展开（见下文）得出。

多重对数函数的导数来自定义的幂级数：

$z{\partial \operatorname {Li} _{s}(z) \over \partial z}=\operatorname {Li} _{s-1}(z)$

${\partial \operatorname {Li} _{s}(e^{\mu }) \over \partial \mu }=\operatorname {Li} _{s-1}(e^{\mu }).$

从级数定义中可以看出平方关系，并且与复制公式有关（参见Clunie (1954)，Schrödinger (1952)）：

$\operatorname {Li} _{s}(-z)+\operatorname {Li} _{s}(z)=2^{1-s}\operatorname {Li} _{s}(z^{2}).$

Kummer函数遵循非常相似的复制公式。对于任何正整数p，这是乘法公式的一个特殊情况：

$\sum _{m=0}^{p-1}\operatorname {Li} _{s}(ze^{2\pi im/p})=p^{1-s}\operatorname {Li} _{s}(z^{p}),$

这可以通过使用多重对数函数的级数定义和指数项的正交性来证明（例如，参见离散傅里叶变换）。

多重对数函数另一个重要的属性，即反演公式，涉及赫尔维茨ζ函数和伯努利多項式，可以在下方与其他函数的关系中找到。

特殊值

在特殊情况下，多重对数函数可用其他函数表示（见下文）。因此多重对数函数的一些特殊值也可用这些函数的特殊值表示。

1. 对于整数阶的多重对数函数，将z·z/∂z算子反复应用于Li₁(z)，即可得到以下的表达式：

$\operatorname {Li} _{1}(z)=-\ln(1-z)$

$\operatorname {Li} _{0}(z)={z \over 1-z}$

$\operatorname {Li} _{-1}(z)={z \over (1-z)^{2}}$

$\operatorname {Li} _{-2}(z)={z(1+z) \over (1-z)^{3}}$

$\operatorname {Li} _{-3}(z)={z(1+4z+z^{2}) \over (1-z)^{4}}$

$\operatorname {Li} _{-4}(z)={z(1+z)(1+10z+z^{2}) \over (1-z)^{5}}.$

因此，对于所有非正整数阶，多重对数函数将退化为关于z的有理分式，因此是关于 z 的有理函数。一般地，可以用有限和来表示：

$\operatorname {Li} _{-n}(z)=\left(z{\partial \over \partial z}\right)^{n}{z \over {1-z}}=\sum _{k=0}^{n}k!S(n+1,k+1)\left({z \over {1-z}}\right)^{k+1}\qquad (n=0,1,2,\ldots ),$

其中S(n,k)是第二类斯特林数。适用于负整数阶的等效的公式为 (Wood 1992)：

$\operatorname {Li} _{-n}(z)=(-1)^{n+1}\sum _{k=0}^{n}k!S(n+1,k+1)\left({{-1} \over {1-z}}\right)^{k+1}\qquad (n=1,2,3,\ldots ),$

或

$\operatorname {Li} _{-n}(z)={1 \over (1-z)^{n+1}}\sum _{k=0}^{n-1}\left\langle {n \atop k}\right\rangle z^{n-k}\qquad (n=1,2,3,\ldots ),$

其中$\scriptstyle \left\langle {n \atop k}\right\rangle$是欧拉数。Li_−n(z)的所有根都是互不相同的实数，并包含z = 0，而其余根为负，并且在对数刻度上以z = -1为中心。随着n变大，对这些有理表达式的数值评估越来越遭受抵消(Wood 1992，§ 6) ；但是，可以通过与Hurwitz zeta函数的一般关系计算Li_-n(z)来获得完全精度（见下文）。

2. 参数z取半整数值时，有：

$\operatorname {Li} _{1}({\tfrac {1}{2}})=\ln 2$

$\operatorname {Li} _{2}({\tfrac {1}{2}})={\tfrac {1}{12}}\pi ^{2}-{\tfrac {1}{2}}(\ln 2)^{2}$

$\operatorname {Li} _{3}({\tfrac {1}{2}})={\tfrac {1}{6}}(\ln 2)^{3}-{\tfrac {1}{12}}\pi ^{2}\ln 2+{\tfrac {7}{8}}\zeta (3),$

其中ζ是黎曼ζ函數。对于更高整数阶，没有这种类型的公式是已知的(Lewin 1991，第2頁)，但是有一个例子 (Borwein, Borwein & Girgensohn 1995)：

$\operatorname {Li} _{4}({\tfrac {1}{2}})={\tfrac {1}{360}}\pi ^{4}-{\tfrac {1}{24}}(\ln 2)^{4}+{\tfrac {1}{24}}\pi ^{2}(\ln 2)^{2}-{\tfrac {1}{2}}\zeta ({\bar {3}},{\bar {1}}),$

其中涉及m和n的二阶交错求和：

$\zeta ({\bar {3}},{\bar {1}})=\sum _{m>n>0}(-1)^{m+n}m^{-3}n^{-1}.$

一般地，对于 n ≥ 2 的整数阶数 (Broadhurst 1996)：

$\operatorname {Li} _{n}({\tfrac {1}{2}})=-\zeta ({\bar {1}},{\bar {1}},\left\{1\right\}^{n-2}),$

其中ζ(s₁,...,s_k)是多ζ函数。比如当 n = 5 时：

$\operatorname {Li} _{5}({\tfrac {1}{2}})=-\zeta ({\bar {1}},{\bar {1}},1,1,1).$

3. 作为级数定义的直接推论，多重对数函数在第 p 个复单位根处的值可由如下傅立叶和给出：

$\operatorname {Li} _{s}(e^{2\pi im/p})=p^{-s}\sum _{k=1}^{p}e^{2\pi imk/p}\zeta (s,{\tfrac {k}{p}})\qquad (m=1,2,\dots ,p-1),$

其中 ζ 是赫尔维茨ζ函数。对于 Re(s) > 1，其中Li _s（1）是有限的，该关系在m = 0或m = p时也成立。尽管此公式并不像下文与其他函数的关系中列出的与Hurwitz zeta函数的更一般的关系所暗示的那样简单，但它的优点是也适用于s的非负整数值。与往常一样，该关系可以被反转来表达ζ（S，M / _P）为任何M = 1，...，P如Li _s的傅立叶总和（EXP（2πiK / _P））超过K = 1，...，p。

与其他函数的关系

• 当 z = 1 时，多重对数函数退化为黎曼ζ函数

$\operatorname {Li} _{s}(1)=\zeta (s)\qquad (\operatorname {Re} (s)>1).$

• 多重对数函数与狄利克雷η函数和狄利克雷β函数有联系：

$\operatorname {Li} _{s}(-1)=-\eta (s),$

其中η(s)是狄利克雷η函数。对于纯虚数的参数，有：

$\operatorname {Li} _{s}(\pm i)=-2^{-s}\eta (s)\pm i\beta (s),$

其中β(s)是狄利克雷β函数。

• 多重对数函数与完全费米-狄拉克积分有关：

$F_{s}(\mu )=-\operatorname {Li} _{s+1}(-e^{\mu }).$

• 多重对数函数是不完全多重对数函数的特例：

$\operatorname {Li} _{s}(z)=\operatorname {Li} _{s}(0,z).$

• 多重对数函数是勒奇超越函数一种特殊情况(Erdélyi et al. 1981，§ 1.11-14)

$\operatorname {Li} _{s}(z)+(-1)^{s}\operatorname {Li} _{s}(1/z)={(2\pi i)^{s} \over \Gamma (s)}~\zeta \left(1-s,~{\frac {1}{2}}+{\ln(-z) \over {2\pi i}}\right),$

• 多重对数函数与赫尔维茨ζ函数的关系如下：

$\operatorname {Li} _{s}(z)={\Gamma (1-s) \over (2\pi )^{1-s}}\left[i^{1-s}\zeta \left(1-s,{\frac {1}{2}}+{\ln(-z) \over {2\pi i}}\right)+i^{s-1}~\zeta \left(1-s,{\frac {1}{2}}-{\ln(-z) \over {2\pi i}}\right)\right],$

但是，哪个关系在伽马函数 Γ（1- s）的极点处在正整数s处无效，而在两个zeta函数的极点处的s = 0处无效。下面的系列表示式给出了该公式的推导。在Hurwitz zeta函数的函数方程的一点帮助下，多重对数函数也因此通过(Jonquière 1889) 与该函数相关：

$i^{-s}\operatorname {Li} _{s}(e^{2\pi ix})+i^{s}\operatorname {Li} _{s}(e^{-2\pi ix})={(2\pi )^{s} \over \Gamma (s)}\zeta (1-s,x),$

其关系式适用于0≤的Re（X）<1，如果IM（X）≥0，和0 <的Re（X）≤1，如果IM（X）<0。 等效地，对于所有的复杂的S和复杂Ž∉] 0; 1]时，反演公式读取

$\operatorname {Li} _{s}(z)+(-1)^{s}\operatorname {Li} _{s}(1/z)={(2\pi i)^{s} \over \Gamma (s)}~\zeta \left(1-s,~{\frac {1}{2}}+{\ln(-z) \over {2\pi i}}\right),$

对于所有的复数 s 和复数 z ∉ ]1;∞[

$\operatorname {Li} _{s}(z)+(-1)^{s}\operatorname {Li} _{s}(1/z)={(2\pi i)^{s} \over \Gamma (s)}~\zeta \left(1-s,~{\frac {1}{2}}-{\ln(-1/z) \over {2\pi i}}\right).$

对于z∉] 0;∞[之一具有LN（- Z）= -ln（- ¹ / _Z），和两个表达式同意。这些关系使多重对数函数的解析连续性超出了收敛圈。z | =定义的幂级数的1。（如果人们假设同时使用多重对数函数和对数的主分支，则Jonquière (1889) 和Erdélyi et al. (1981) 的相应方程式是不正确的。）如果s是整数，请参见下一项以获取简化公式。

• 对于正整数阶数s，赫尔维茨ζ函数 ζ(1-s,x) 简化为伯努利多項式，ζ(1-n,x) = -B_n(x)/n，而 n = 1, 2, 3, ...时的Jonquière反演公式则变为：

$\operatorname {Li} _{n}(e^{2\pi ix})+(-1)^{n}\operatorname {Li} _{n}(e^{-2\pi ix})=-{(2\pi i)^{n} \over n!}B_{n}(x),$

其中再次0≤的Re（X）<1，如果IM（X）≥0，和0 <的Re（X）≤1，如果IM（X）<0。 将多重对数函数参数限制为单位圆Im（x）= 0时，如果n为偶数，则该公式的左侧简化为2 Re（Li _n（e ^{2 ixix}）），并简化为2 i Im（Li如果n为奇数，^则为 _n（e ^2πix）。对于负整数的订单，在另一方面，Γ（多个）的发散意味着所有的Z那(Erdélyi et al. 1981)

$\operatorname {Li} _{-n}(z)+(-1)^{n}\operatorname {Li} _{-n}(1/z)=0\qquad (n=1,2,3,\ldots ).$

更一般地，对于 n ＝ 0, ±1, ±2, ±3, ...，有：

$\operatorname {Li} _{n}(z)+(-1)^{n}\operatorname {Li} _{n}(1/z)=-{\frac {(2\pi i)^{n}}{n!}}B_{n}\left({\frac {1}{2}}+{\ln(-z) \over {2\pi i}}\right)\qquad (z\not \in ]0;1]),$

$\operatorname {Li} _{n}(z)+(-1)^{n}\operatorname {Li} _{n}(1/z)=-{\frac {(2\pi i)^{n}}{n!}}B_{n}\left({\frac {1}{2}}-{\ln(-1/z) \over {2\pi i}}\right)\qquad (z\not \in ~]1;\infty [),$

其中两个表达式同意针对z∉] 0;∞[。（Jonquière (1889) 和Erdélyi et al. (1981) 的相应方程式也不正确。）

• 具有纯虚数μ的多重对数函数可以用克劳森函数 Ci_s(θ)和Si_s(θ)表示，反之亦然（Lewin 1958 Abramowitz & Stegun 1972 ； Abramowitz & Stegun 1972）：

$\operatorname {Li} _{s}(e^{\pm i\theta })=Ci_{s}(\theta )\pm iSi_{s}(\theta ).$

• 反正切积分 Ti_s(z) (Lewin 1958) 可以用多重对数函数表示：

$\operatorname {Ti} _{s}(z)={1 \over 2i}\left[\operatorname {Li} _{s}(iz)-\operatorname {Li} _{s}(-iz)\right].$

该关系特别暗示：

$\operatorname {Ti} _{0}(z)={z \over 1+z^{2}},\quad \operatorname {Ti} _{1}(z)=\arctan z,\quad \operatorname {Ti} _{2}(z)=\int _{0}^{z}{\arctan t \over t}dt,\quad \ldots ~\quad \operatorname {Ti} _{n+1}(z)=\int _{0}^{z}{\frac {\operatorname {Ti} _{n}(t)}{t}}dt,$

这说明了这个函数的名称

• 勒让德χ函数 χ_sz（Lewin 1958 Boersma & Dempsey 1992）可以用多重对数函数表示：

$\chi _{s}(z)={\tfrac {1}{2}}\left[\operatorname {Li} _{s}(z)-\operatorname {Li} _{s}(-z)\right].$

• 整数阶的多重对数函数可以用广义超几何函数表示：

$\operatorname {Li} _{n}(z)=z_{n+1}F_{n}(1,1,\dots ,1;2,2,\dots ,2;z)\qquad (n=0,1,2,\ldots ),$

$\operatorname {Li} _{-n}(z)=z_{n}F_{n-1}(2,2,\dots ,2;1,1,\dots ,1;z)\qquad (n=1,2,3,\ldots )~.$

• 不完全黎曼ζ函數“德拜函数”而言（(Abramowitz & Stegun 1972)）：

$Z_{n}(z)={1 \over (n-1)!}\int _{z}^{\infty }{t^{n-1} \over e^{t}-1}dt\qquad (n=1,2,3,\ldots ),$

正整数阶的多重对数函数Li_n(z)可用有限和表示(Wood 1992):

$\operatorname {Li} _{n}(e^{\mu })=\sum _{k=0}^{n-1}Z_{n-k}(-\mu ){\mu ^{k} \over k!}\qquad (n=1,2,3,\ldots ).$

一个非常相似的表达式将“德拜函数”Z_n(z) 与多重对数函数联系在了一起：

$Z_{n}(z)=\sum _{k=0}^{n-1}\operatorname {Li} _{n-k}(e^{-z}){z^{k} \over k!}\qquad (n=1,2,3,\ldots ).$

积分表示

以下任何一个积分表示形式都可以使多重对数函数的解析连续性超出收敛圆| z | =定义的幂级数的1。

1 可以使用玻色–爱因斯坦分布的积分表示多重对数函数：

$\operatorname {Li} _{s}(z)={1 \over \Gamma (s)}\int _{0}^{\infty }{t^{s-1} \over e^{t}/z-1}dt.$

当 Re(s) > 0 且 z 非 z ≥ 1 的实数时，上式收敛。在这种情况下，多重对数函数有时会被称为玻色积分，但更常被称为玻色–爱因斯坦积分。类似地，多重对数函数也可以用费米-狄拉克分布的积分表示：

$-\operatorname {Li} _{s}(-z)={1 \over \Gamma (s)}\int _{0}^{\infty }{t^{s-1} \over e^{t}/z+1}dt.$

当 Re(s) > 0 且 z 非 z ≤ -1 的实数时，上式收敛。在这种情况下，多重对数函数有时也被称为费米积分或费米-狄拉克积分(GSL 2010)。这些表示可以容易地通过被击函数关于z的泰勒级数的逐项积分进行验证。Dingle 的论文包含对两种类型积分的详细研究。

多重对数函数还与麦克斯韦-玻尔兹曼分布的积分有关：

$\lim _{z\to 0}{\frac {\operatorname {Li} _{s}(z)}{z}}={1 \over \Gamma (s)}\int _{0}^{\infty }{t^{s-1}e^{-t}}dt=1.$

这也给出了多重对数函数在原点附近的渐近性质。

2. complementary integral表示适用于 Re(s) < 0 和所有除了非 z ≥ 0 的实数：

$\operatorname {Li} _{s}(z)=\int _{0}^{\infty }{t^{-s}\sin[s\pi /2-t\ln(-z)] \over \sinh(\pi t)}dt.$

该积分来自多重对数函数与赫尔维茨ζ函数的一般关系（请参见上文）和后者的常见积分表示。

3. 多重对数函数通常可以由汉克轮廓积分表示(Whittaker & Watson 1927，§ 12.22, § 13.13)，该方程将Bose-Einstein表示扩展到负阶s。只要被整数的t = μ 极不位于非负实轴上，并且s ≠1、2、3，...，就有：

$\operatorname {Li} _{s}(e^{\mu })=-{{\Gamma (1-s)} \over {2\pi i}}\oint _{H}{{(-t)^{s-1}} \over {e^{t-\mu }-1}}dt$

其中H代表汉克尔轮廓。被积物沿实轴具有从零到无穷大的切口，该轴属于t的下半平面。积分从上半平面的+∞开始（Im（t）>   0），绕圈原点而不包围任何极点t = µ + 2kπi，并在下半平面（Im（t）<   0）。对于µ为实数且为非负数的情况，我们可以简单地减去封闭的t = µ极点的贡献：

$\operatorname {Li} _{s}(e^{\mu })=-{{\Gamma (1-s)} \over {2\pi i}}\oint _{H}{{(-t)^{s-1}} \over {e^{t-\mu }}-1}dt-2\pi iR$

其中R是极点的残基 ：

$R={i \over 2\pi }\Gamma (1-s)(-\mu )^{s-1}.$

4. 当将Abel–Plana公式应用于多重对数函数的定义级数时，将生成夏爾·埃爾米特型积分表示形式，该表示形式对于所有复数z和所有复数s有效 ：

$\operatorname {Li} _{s}(z)={\tfrac {1}{2}}z+{\Gamma (1-s,-\ln z) \over (-\ln z)^{1-s}}+2z\int _{0}^{\infty }{\frac {\sin(s\arctan t-t\ln z)}{(1+t^{2})^{s/2}(e^{2\pi t}-1)}}dt$

其中Γ是上不完全Γ函数。此表达式中的全部（但不是全部）ln(z)都可以替换为-ln（¹ ⁄ _z）。一个相关的表示形式，对于所有s，

$\operatorname {Li} _{s}(z)={\tfrac {1}{2}}z+z\int _{0}^{\infty }{\frac {\sin[s\arctan t-t\ln(-z)]}{(1+t^{2})^{s/2}\sinh(\pi t)}}dt,$

避免使用不完全伽玛功能，但针对z这个积分失败。如果再（S）正实轴≤   0。该表达式可通过将 2^s Li_s(−z) / (−z) 改写为 Φ(z², s, ¹⁄₂) − z Φ(z², s, 1) 得到，其中 Φ 是勒奇超越函数，将 Abel–Plana 公式应用于第一个 Φ 的级数，并使用一个包含第二个Φ系列的1 /（e ^2πt +1）代替1 /（e ^2πt− 1）的互补公式。

5， 如在引用的我们可以通过积分普通表达的组成为多重对数函数几何级数逐项为$s\in \mathbb {N}$如

$\operatorname {Li} _{s+1}(z)={\frac {z\cdot (-1)^{s}}{s!}}\int _{0}^{1}{\frac {\log ^{s}(t)}{1-tz}}dt.$

级数表示

1. 如上文积分表示中所指出的，可以通过汉克等高线积分的方式将多重对数函数的玻色–爱因斯坦积分表示扩展到负阶s：

$\operatorname {Li} _{s}(e^{\mu })=-{\Gamma (1-s) \over 2\pi i}\oint _{H}{(-t)^{s-1} \over e^{t-\mu }-1}dt,$

其中H是汉克尔等高线，s ≠1，2，3，...，并且被积物的t = μ极不位于非负实轴上。所述轮廓可以这样进行修饰，它包围所述磁极在t被积函数- μ= 2kπi，积分可以被评估为的总和残基（Wood 1992 Gradshteyn & Ryzhik 1980）：

$\operatorname {Li} _{s}(e^{\mu })=\Gamma (1-s)\sum _{k=-\infty }^{\infty }(2k\pi i-\mu )^{s-1}.$

这对Re(s) < 0和除了e^μ = 1 的μ成立。当0 < Im(µ) ≤ 2π 时，该和式可被拆分为：

$\operatorname {Li} _{s}(e^{\mu })=\Gamma (1-s)\left[(-2\pi i)^{s-1}\sum _{k=0}^{\infty }\left(k+{\mu \over {2\pi i}}\right)^{s-1}+(2\pi i)^{s-1}\sum _{k=0}^{\infty }\left(k+1-{\mu \over {2\pi i}}\right)^{s-1}\right],$

两个级数可以用赫尔维茨ζ函数表示：

$\operatorname {Li} _{s}(e^{\mu })={\Gamma (1-s) \over (2\pi )^{1-s}}\left[i^{1-s}~\zeta \left(1-s,~{\mu \over {2\pi i}}\right)+i^{s-1}~\zeta \left(1-s,~1-{\mu \over {2\pi i}}\right)\right]\qquad (0<\operatorname {Im} (\mu )\leq 2\pi ).$

该关系已经根据在上文其他函数的关系中给出，对所有满足 s ≠ 0, 1, 2, 3, ... 的复数s都成立，并首先在(Jonquière 1889)被推导。

2. 为了将多重对数函数表示为μ = 0的幂级数，我们将从汉克轮廓积分导出的级数写为：

$\operatorname {Li} _{s}(e^{\mu })=\Gamma (1-s)(-\mu )^{s-1}+\Gamma (1-s)\sum _{h=1}^{\infty }\left[(-2h\pi i-\mu )^{s-1}+(2h\pi i-\mu )^{s-1}\right].$

当和中的二项式幂展开约µ = 0且求和的顺序相反时，h上的和可以用封闭形式表示：

$\operatorname {Li} _{s}(e^{\mu })=\Gamma (1-s)(-\mu )^{s-1}+\sum _{k=0}^{\infty }{\zeta (s-k) \over k!}\mu ^{k}.$

此结果适用于| µ | <2π，并且由于由所提供的解析开拓zeta函数，对于所有s≠1，2，3，。。。。如果阶数为正整数s = n，则k = n − 1的项和伽马函数都变为无穷大，尽管它们的总和不是。一个获得（Wood 1992  ; Gradshteyn & Ryzhik 1980）：

$\lim _{s\to k+1}\left[{\zeta (s-k) \over k!}\mu ^{k}+\Gamma (1-s)(-\mu )^{s-1}\right]={\mu ^{k} \over k!}\left[\sum _{h=1}^{k}{1 \over h}-\ln(-\mu )\right],$

如果k = 0，则h上的总和消失。因此，对于正整数阶和μ | <2π，我们有系列：

$\operatorname {Li} _{n}(e^{\mu })={\mu ^{n-1} \over (n-1)!}\left[H_{n-1}-\ln(-\mu )\right]+\sum _{k=0,k\neq n-1}^{\infty }{\zeta (n-k) \over k!}\mu ^{k},$

其中H_n表示第n个谐波数 ：

$H_{n}=\sum _{h=1}^{n}{1 \over h},\qquad H_{0}=0.$

问题术语现在包含-ln（- μ），当由μn倍^-1，将趋 向于零，μ→0，除了n = 1 的。这反映了一个事实，即Li _s (z)在s = 1和z = 1时表现出对数奇异性，因为：

$\lim _{\mu \to 0}\Gamma (1-s)(-\mu )^{s-1}=0\qquad (\operatorname {Re} (s)>1).$

对于接近但不等于正整数的s，可以期望展开在µ = 0处的发散项会导致计算困难(Wood 1992)。ERDELYI的相应的扩展(Erdélyi et al. 1981) 在LN（z）的权力是不正确的，如果一个假定多重对数函数和对数的主要分支被同时使用，因为^LN（1 / _z）为不均匀等于-ln(z)。

对于s的非正整数值，展开约µ = 0时的zeta函数ζ(s- k）减小为伯努利数 ：ζ（-n - k）= -B _{1+ n + k} /（1 + n + k）。通过该系列进行的Li _{- n} (z)的数值评估不会受到抵消效应的影响，在上述特定值下给出的有限有理表达式对于n较大。

3. 通过使用单位元

$1={1 \over \Gamma (s)}\int _{0}^{\infty }e^{-t}t^{s-1}dt\qquad (\operatorname {Re} (s)>0),$

多重对数函数的 Bose-Einstein 积分表示形式（见上文）可以转换为以下形式：

$\operatorname {Li} _{s}(z)={\tfrac {1}{2}}z+{z \over 2\Gamma (s)}\int _{0}^{\infty }e^{-t}t^{s-1}\coth {t-\ln z \over 2}dt\qquad (\operatorname {Re} (s)>0).$

将双曲余切项展开为双边级数，

$\coth {t-\ln z \over 2}=2\sum _{k=-\infty }^{\infty }{1 \over 2k\pi i+t-\ln z},$

然后反转积分和的顺序，最后用上不完全Γ函数的积分表示来识别被加数，可以得到：

$\operatorname {Li} _{s}(z)={\tfrac {1}{2}}z+\sum _{k=-\infty }^{\infty }{\Gamma (1-s,2k\pi i-\ln z) \over (2k\pi i-\ln z)^{1-s}}.$

对于该结果的双侧级数和双曲余切线，从-k _max到k _max的对称部分和无条件地收敛为k _max →∞。如果求和是对称进行的，那么对于Li _s (z)的该级数对所有复数s和所有复数z都成立。

4。 可以将第二种斯特林数的显式引入非正整数阶多重对数函数的有限和中（见上文），可以这样写：

$\operatorname {Li} _{-n}(z)=\sum _{k=0}^{n}\left({-z \over 1-z}\right)^{k+1}\sum _{j=0}^{k}(-1)^{j+1}{k \choose j}(j+1)^{n}\qquad (n=0,1,2,\ldots ).$

通过简单地将外部求和扩展为∞而获得的无穷级数(Guillera & Sondow 2008) ：

$\operatorname {Li} _{s}(z)=\sum _{k=0}^{\infty }\left({-z \over 1-z}\right)^{k+1}~\sum _{j=0}^{k}(-1)^{j+1}{k \choose j}(j+1)^{-s},$

原来收敛到多重对数函数的所有复杂的S和用于与的Re（z）的复杂^_Ž<1/2，由于可以验证为| ^{− z} ⁄ _{（1− z）} | < ^{_二分之一}通过反转求和并使用的顺序：

$\sum _{k=j}^{\infty }{k \choose j}\left({-z \over 1-z}\right)^{k+1}=\left[\left({-z \over 1-z}\right)^{-1}-1\right]^{-j-1}=(-z)^{j+1}.$

这些序列的内系数可以由涉及广义谐波数的 斯特林数相关公式表示。例如，请参见生成函数转换以查找以下身份的证明（对证明的引用）：

${\begin{aligned}\operatorname {Li} _{2}(z)&=\sum _{j\geq 1}{\frac {(-1)^{j-1}}{2}}\left(H_{j}^{2}+H_{j}^{(2)}\right){\frac {z^{j}}{(1-z)^{j+1}}}\\\operatorname {Li} _{3}(z)&=\sum _{j\geq 1}{\frac {(-1)^{j-1}}{6}}\left(H_{j}^{3}+3H_{j}H_{j}^{(2)}+2H_{j}^{(3)}\right){\frac {z^{j}}{(1-z)^{j+1}}}.\end{aligned}}$

对于随Re（z）的其他参数^_<1/2中的结果通过如下解析开拓。此过程等效于将Euler变换应用于z中定义多重对数函数的序列。

渐近展开

对于 |z| ≫ 1，可以根据ln(−z)将多重对数函数展开为渐近级数 ：

$\operatorname {Li} _{s}(z)={\pm i\pi \over \Gamma (s)}[\ln(-z)\pm i\pi ]^{s-1}-\sum _{k=0}^{\infty }(-1)^{k}(2\pi )^{2k}{B_{2k} \over (2k)!}{[\ln(-z)\pm i\pi ]^{s-2k} \over \Gamma (s+1-2k)},$

$\operatorname {Li} _{s}(z)=\sum _{k=0}^{\infty }(-1)^{k}(1-2^{1-2k})(2\pi )^{2k}{B_{2k} \over (2k)!}{[\ln(-z)]^{s-2k} \over \Gamma (s+1-2k)},$

其中 B_2k 是伯努利数。两个式子对于所有s和任何arg(z)都成立。像往常一样，当项的大小开始增长时，应终止求和。对于负整数s，展开完全消失；对于非负整数s，它们在有限数量的项之后分解。Wood (1992) 描述了一种用于从玻色-爱因斯坦积分表示获得这些系列的方法（他的方程11.2栗_{'^S（Ëμ）'}要求'-2π<IM（μ）≤0）。'

极限性质

以下极限可以由多重对数函数的各种表示形式推导得到(Wood 1992)：

$\lim _{|z|\to 0}\operatorname {Li} _{s}(z)=z$

$\lim _{|\mu |\to 0}\operatorname {Li} _{s}(e^{\mu })=\Gamma (1-s)(-\mu )^{s-1}\qquad (\operatorname {Re} (s)<1)$

$\lim _{\operatorname {Re} (\mu )\to \infty }\operatorname {Li} _{s}(e^{\mu })=-{\mu ^{s} \over \Gamma (s+1)}\qquad (s\neq -1,-2,-3,\ldots )$

$\lim _{\operatorname {Re} (\mu )\to \infty }\operatorname {Li} _{-n}(e^{\mu })=-(-1)^{n}e^{-\mu }\qquad (n=1,2,3,\ldots )$

$\lim _{\operatorname {Re} (s)\to \infty }\operatorname {Li} _{s}(z)=z$

$\lim _{\operatorname {Re} (s)\to -\infty }\operatorname {Li} _{s}(e^{\mu })=\Gamma (1-s)(-\mu )^{s-1}\qquad (-\pi <\operatorname {Im} (\mu )<\pi )$

$\lim _{\operatorname {Re} (s)\to -\infty }\operatorname {Li} _{s}(-e^{\mu })=\Gamma (1-s)\left[(-\mu -i\pi )^{s-1}+(-\mu +i\pi )^{s-1}\right]\qquad (\operatorname {Im} (\mu )=0)$

Wood 关于的 Re(µ)→∞的第一极限已根据他的方程11.3进行了校正。Re(s)→-∞的极限来自于多重对数函数与赫尔维茨ζ函数的一般关系（参见上文）。

二重对数函数

主条目：二重对数函数

二重对数函数是阶数 s = 2 的多重对数函数。对任意复数参数z，二重对数函数也可用积分表达式表示(Abramowitz & Stegun 1972) §27.7 ：

$\operatorname {Li} _{2}(z)=-\int _{0}^{z}{\ln(1-t) \over t}dt=-\int _{0}^{1}{\ln(1-zt) \over t}dt.$

造成混淆的一个原因是某些计算机代数系统将对数定义为dilog(z)= Li ₂（1- z）。

在re(z)≥1情况下为二重对数函数的第一个积分式可写成

$\operatorname {Li} _{2}(z)={\frac {\pi ^{2}}{6}}-\int _{1}^{z}{\ln(t-1) \over t}dt-i\pi \ln z$

将ln（t -1）展开，并逐项积分，我们得到

$\operatorname {Li} _{2}(z)={\frac {\pi ^{2}}{3}}-{\frac {1}{2}}(\ln z)^{2}-\sum _{k=1}^{\infty }{1 \over k^{2}z^{k}}-i\pi \ln z\qquad (z\geq 1).$

二重对数函数的阿贝尔恒等式由(Abel 1881) 给出

$\operatorname {Li} _{2}\left({\frac {x}{1-y}}\right)+\operatorname {Li} _{2}\left({\frac {y}{1-x}}\right)-\operatorname {Li} _{2}\left({\frac {xy}{(1-x)(1-y)}}\right)=\operatorname {Li} _{2}(x)+\operatorname {Li} _{2}(y)+\ln(1-x)\ln(1-y)$

$(\operatorname {Re} (x)\leq {\tfrac {1}{2}}\wedge \operatorname {Re} (y)\leq {\tfrac {1}{2}}\vee \operatorname {Im} (x)>0\wedge \operatorname {Im} (y)>0\vee \operatorname {Im} (x)<0\wedge \operatorname {Im} (y)<0\vee \ldots ).$

这立即看到搁置要么X = 0或y = 0，而对于一般的参数，然后很容易地分化'∂/∂X∂/∂ÿ'验证。对于y = 1- x，恒等式简化为欧拉 反射公式

$\operatorname {Li} _{2}\left(x\right)+\operatorname {Li} _{2}\left(1-x\right)={\frac {1}{6}}\pi ^{2}-\ln(x)\ln(1-x),$

其中，Li 2（1）=ζ（2）= 1/6的 π2已被使用，并且x可以采取任何复数值。

根据新变量u = x /（1- y），v = y /（1- x），Abel身份读取

$\operatorname {Li} _{2}(u)+\operatorname {Li} _{2}(v)-\operatorname {Li} _{2}(uv)=\operatorname {Li} _{2}\left({\frac {u-uv}{1-uv}}\right)+\operatorname {Li} _{2}\left({\frac {v-uv}{1-uv}}\right)+\ln \left({\frac {1-u}{1-uv}}\right)\ln \left({\frac {1-v}{1-uv}}\right),$

对应于(Rogers 1907) 给出的五边形标识。

根据x = y = 1- z的Abel身份和平方关系，我们得到Landen的身份

$\operatorname {Li} _{2}(1-z)+\operatorname {Li} _{2}\left(1-{\frac {1}{z}}\right)=-{\frac {1}{2}}(\ln z)^{2}\qquad (z\not \in ~]-\infty ;0]),$

并将反射公式应用于每个对数，我们找到反演公式

$\operatorname {Li} _{2}(z)+\operatorname {Li} _{2}(1/z)=-{\tfrac {1}{6}}\pi ^{2}-{\tfrac {1}{2}}[\ln(-z)]^{2}\qquad (z\not \in [0;1[),$

和真正的z ≥ 1 还

$\operatorname {Li} _{2}(z)+\operatorname {Li} _{2}(1/z)={\tfrac {1}{3}}\pi ^{2}-{\tfrac {1}{2}}(\ln z)^{2}-i\pi \ln z.$

下表中收集了特殊参数对数的已知封闭式评估。在第一列中的参数由反射相关X↔1- x或反转^X↔1 / _x至任一X = 0或X = -1;这些操作将第三列中的参数相互关联。

Maximon (2003) discusses the 17th to 19th century references. The reflection formula was already published by Landen in 1760, prior to its appearance in a 1768 book by Euler (Maximon 2003); an equivalent to Abel's identity was already published by Spence in 1809, before Abel wrote his manuscript in 1826 (Zagier 1989). The designation bilogarithmische Function was introduced by Carl Johan Danielsson Hill (professor in Lund, Sweden) in 1828 (Maximon 2003).  （1989） has remarked that the dilogarithm is the only mathematical function possessing a sense of humor.

二重对数函数的特殊值

$x$	$\operatorname {Li} _{2}(x)$	$x$	$\operatorname {Li} _{2}(x)$
$-1$	$-{\tfrac {1}{12}}\pi ^{2}$	$-\phi$	$-{\tfrac {1}{10}}\pi ^{2}-\ln ^{2}\phi$
$0$	$0$	$-1/\phi$	$-{\tfrac {1}{15}}\pi ^{2}+{\tfrac {1}{2}}\ln ^{2}\phi$
${\tfrac {1}{2}}$	${\tfrac {1}{12}}\pi ^{2}-{\tfrac {1}{2}}\ln ^{2}2$	$1/\phi ^{2}$	${\tfrac {1}{15}}\pi ^{2}-\ln ^{2}\phi$
$1$	${\tfrac {1}{6}}\pi ^{2}$	$1/\phi$	${\tfrac {1}{10}}\pi ^{2}-\ln ^{2}\phi$
$2$	${\tfrac {1}{4}}\pi ^{2}-\pi i\ln 2$	$\phi$	${\tfrac {11}{15}}\pi ^{2}+{\tfrac {1}{2}}\ln ^{2}(-1/\phi )$
		$\phi ^{2}$	$-{\tfrac {11}{15}}\pi ^{2}-\ln ^{2}(-\phi )$

这里的 $\phi ={\tfrac {1}{2}}({\sqrt {5}}+1)$ 表示黄金比例.

多重对数函数阶梯

伦纳德·莱文（Leonard Lewin）在特殊值的多重对数上发现了许多经典关系的显着而广泛的概括。这些现在称为多重对数函数阶梯。定义$\rho ={\tfrac {1}{2}}({\sqrt {5}}-1)$作为黄金比例的倒数。然后是对数阶梯的两个简单示例

$\operatorname {Li} _{2}(\rho ^{6})=4\operatorname {Li} _{2}(\rho ^{3})+3\operatorname {Li} _{2}(\rho ^{2})-6\operatorname {Li} _{2}(\rho )+{\tfrac {7}{30}}\pi ^{2}$

这由 Coxeter （1935）给出，和

$\operatorname {Li} _{2}(\rho )={\tfrac {1}{10}}\pi ^{2}-\ln ^{2}\rho$

由兰登给出。多重对数函数梯子自然而深地出现在K理论和代数几何中。多重对数函数阶梯为通过BBP算法快速计算各种数学常数提供了基础(Bailey, Borwein & Plouffe 1997)。

单值性

多重对数函数有两个分支点，它们分别位于 z = 1 和 z = 0 处。z = 0 处的第二个分支点在多重对数函数的主表上不可见；仅当该功能在分析上继续到其其他图纸时，它才可见。多重对数函数的单峰组由围绕两个分支点缠绕的同型类循环组成。用m ₀和m ₁表示这两个，单峰组具有组表示

$\langle m_{0},m_{1}\vert w=m_{0}m_{1}m_{0}^{-1}m_{1}^{-1},wm_{1}=m_{1}w\rangle .$

对于二重对数函数的特殊情况，也有wm ₀ = m ₀ w，单峰组成为Heisenberg组（用x，y，z标识m ₀，m ₁和w）(Vepstas 2008)。

参考资料

• Abel, N.H. http://www.abelprisen.no/nedlastning/verker/oeuvres_1881_del2/oeuvres_completes_de_abel_nouv_ed_2_kap14_opt.pdf (PDF). Sylow, L.; Lie, S. (编). Œuvres complètes de Niels Henrik Abel − Nouvelle édition, Tome II. Christiania [Oslo]: Grøndahl & Søn. 1881: 189–193 [1826] （French）.  引文格式1维护：未识别语文类型 (link) (this 1826 manuscript was only published posthumously.)
• Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover Publications. 1972. ISBN 978-0-486-61272-0. 
• Apostol, T.M. (2010), "Polylogarithm", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248CS1 maint: ref=harv (link)
• Bailey, D.H.; Borwein, P.B.; Plouffe, S. On the Rapid Computation of Various Polylogarithmic Constants (PDF). Mathematics of Computation. April 1997, 66 (218): 903–913. Bibcode:1997MaCom..66..903B. doi:10.1090/S0025-5718-97-00856-9. 
• Bailey. A Seventeenth-Order Polylogarithm Ladder. 
• Berndt, B.C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag. 1994: 323–326. ISBN 978-0-387-94109-7. 
• Boersma, J.; Dempsey, J.P. On the evaluation of Legendre's chi-function. Mathematics of Computation. 1992, 59 (199): 157–163. JSTOR 2152987. doi:10.2307/2152987. 
• Borwein, D.; Borwein, J.M.; Girgensohn, R. Explicit evaluation of Euler sums (PDF). Proceedings of the Edinburgh Mathematical Society. Series 2. 1995, 38 (2): 277–294. doi:10.1017/S0013091500019088. 
• Borwein, J.M.; Bradley, D.M.; Broadhurst, D.J.; Lisonek, P. Special Values of Multiple Polylogarithms. Transactions of the American Mathematical Society. 2001, 353 (3): 907–941. arXiv:math/9910045 . doi:10.1090/S0002-9947-00-02616-7. 
• Broadhurst. On the enumeration of irreducible k-fold Euler sums and their roles in knot theory and field theory. 
• Clunie, J. On Bose-Einstein functions. Proceedings of the Physical Society. Series A. 1954, 67 (7): 632–636. Bibcode:1954PPSA...67..632C. doi:10.1088/0370-1298/67/7/308. 
• Cohen, H.; Lewin, L.; Zagier, D. A Sixteenth-Order Polylogarithm Ladder (PS). Experimental Mathematics. 1992, 1 (1): 25–34. 
• Coxeter, H.S.M. The functions of Schläfli and Lobatschefsky. Quarterly Journal of Mathematics (Oxford). 1935, 6 (1): 13–29. Bibcode:1935QJMat...6...13C. JFM 61.0395.02. doi:10.1093/qmath/os-6.1.13. 
• Cvijovic, D.; Klinowski, J. Continued-fraction expansions for the Riemann zeta function and polylogarithms (PDF). Proceedings of the American Mathematical Society. 1997, 125 (9): 2543–2550. doi:10.1090/S0002-9939-97-04102-6. 
• Cvijovic, D. New integral representations of the polylogarithm function. Proceedings of the Royal Society A. 2007, 463 (2080): 897–905. Bibcode:2007RSPSA.463..897C. arXiv:0911.4452 . doi:10.1098/rspa.2006.1794. 
• Erdélyi, A.; Magnus, W.; Oberhettinger, F.; Tricomi, F.G. Higher Transcendental Functions, Vol. 1 (PDF). Malabar, FL: R.E. Krieger Publishing. 1981. ISBN 978-0-89874-206-0.  (this is a reprint of the McGraw–Hill original of 1953.)
• Fornberg, B.; Kölbig, K.S. Complex zeros of the Jonquière or polylogarithm function. Mathematics of Computation. 1975, 29 (130): 582–599. JSTOR 2005579. doi:10.2307/2005579. 
• GNU Scientific Library. Reference Manual. 2010 [2010-06-13]. 
• Gradshteyn, Izrail Solomonovich; Ryzhik, Iosif Moiseevich; Geronimus, Yuri Veniaminovich; Tseytlin, Michail Yulyevich; Jeffrey, Alan; Moll. Zwillinger, Victor Hugo , 编. 9.553. 8. Academic Press, Inc. 2015: 1050 [October 2014]. ISBN 978-0-12-384933-5. LCCN 2014010276 （English）.  引文格式1维护：未识别语文类型 (link)
• Guillera, J.; Sondow, J. Double integrals and infinite products for some classical constants via analytic continuations of Lerch's transcendent. The Ramanujan Journal. 2008, 16 (3): 247–270. arXiv:math.NT/0506319 . doi:10.1007/s11139-007-9102-0. 
• Hain. Classical polylogarithms. 
• Jahnke, E.; Emde, F. Tables of Functions with Formulae and Curves 4th. New York: Dover Publications. 1945. 
• Jonquière, A. Note sur la série $\scriptstyle \sum _{n=1}^{\infty }{\frac {x^{n}}{n^{s}}}$ (PDF). Bulletin de la Société Mathématique de France. 1889, 17: 142–152. JFM 21.0246.02. doi:10.24033/bsmf.392 （French）.  引文格式1维护：未识别语文类型 (link)
• Kölbig, K.S.; Mignaco, J.A.; Remiddi, E. On Nielsen's generalized polylogarithms and their numerical calculation. BIT. 1970, 10: 38–74. doi:10.1007/BF01940890. 
• Kirillov, A.N. Dilogarithm identities. Progress of Theoretical Physics Supplement. 1995, 118: 61–142. Bibcode:1995PThPS.118...61K. arXiv:hep-th/9408113 . doi:10.1143/PTPS.118.61. 
• Lewin, L. Dilogarithms and Associated Functions. London: Macdonald. 1958. MR 0105524. 
• Lewin, L. Polylogarithms and Associated Functions. New York: North-Holland. 1981. ISBN 978-0-444-00550-2. 
• Lewin, L. (编). Structural Properties of Polylogarithms. Mathematical Surveys and Monographs 37. Providence, RI: Amer. Math. Soc. 1991. ISBN 978-0-8218-1634-9. 
• Markman, B. The Riemann Zeta Function. BIT. 1965, 5: 138–141. 
• Maximon, L.C. The Dilogarithm Function for Complex Argument. Proceedings of the Royal Society A. 2003, 459 (2039): 2807–2819. Bibcode:2003RSPSA.459.2807M. doi:10.1098/rspa.2003.1156. 
• McDougall, J.; Stoner, E.C. The computation of Fermi-Dirac functions. Philosophical Transactions of the Royal Society A. 1938, 237 (773): 67–104. Bibcode:1938RSPTA.237...67M. JFM 64.1500.04. doi:10.1098/rsta.1938.0004. 
• Nielsen, N. Der Eulersche Dilogarithmus und seine Verallgemeinerungen. Eine Monographie. Nova Acta Leopoldina (Halle – Leipzig, Germany: Kaiserlich-Leopoldinisch-Carolinische Deutsche Akademie der Naturforscher). 1909, XC (3): 121–212. JFM 40.0478.01 （German）.  引文格式1维护：未识别语文类型 (link)
• Prudnikov, A.P.; Marichev, O.I.; Brychkov, Yu.A. Integrals and Series, Vol. 3: More Special Functions. Newark, NJ: Gordon and Breach. 1990. ISBN 978-2-88124-682-1.  (see § 1.2, "The generalized zeta function, Bernoulli polynomials, Euler polynomials, and polylogarithms", p. 23.)
• Robinson, J.E. Note on the Bose-Einstein integral functions. Physical Review. Series 2. 1951, 83 (3): 678–679. Bibcode:1951PhRv...83..678R. doi:10.1103/PhysRev.83.678. 
• Rogers, L.J. On function sum theorems connected with the series $\scriptstyle \sum _{n=1}^{\infty }{\frac {x^{n}}{n^{2}}}$. Proceedings of the London Mathematical Society (2). 1907, 4 (1): 169–189. JFM 37.0428.03. doi:10.1112/plms/s2-4.1.169. 
• Schrödinger, E. Statistical Thermodynamics 2nd. Cambridge, UK: Cambridge University Press. 1952. 
• Truesdell, C. On a function which occurs in the theory of the structure of polymers. Annals of Mathematics. Second Series. 1945, 46 (1): 144–157. JSTOR 1969153. doi:10.2307/1969153. 
• Vepstas, L. An efficient algorithm for accelerating the convergence of oscillatory series, useful for computing the polylogarithm and Hurwitz zeta functions. Numerical Algorithms. 2008, 47 (3): 211–252. Bibcode:2008NuAlg..47..211V. arXiv:math.CA/0702243 . doi:10.1007/s11075-007-9153-8. 
• Whittaker, E.T.; Watson, G.N. A Course of Modern Analysis 4th. Cambridge, UK: Cambridge University Press. 1927.  (this edition has been reprinted many times, a 1996 paperback has ISBN 0-521-09189-6.)
• Wirtinger, W. Über eine besondere Dirichletsche Reihe. Journal für die Reine und Angewandte Mathematik. 1905, 1905 (129): 214–219. JFM 37.0434.01. doi:10.1515/crll.1905.129.214 （German）.  引文格式1维护：未识别语文类型 (link)
• Wood, D.C. The Computation of Polylogarithms. Technical Report 15-92* (PS). University of Kent Computing Laboratory. June 1992 [2005-11-01]. 
• Zagier, D. Studies in Mathematics.  (also appeared as "The remarkable dilogarithm" in Journal of Mathematical and Physical Sciences 22 (1988), pp. 131–145, and as Chapter I of (Zagier 2007).)
• Zagier, D. http://mathlab.snu.ac.kr/~top/articles/zagier.pdf (PDF). Cartier, P.E.; Julia, B.; Moussa, P.; Vanhove, P. (编). Frontiers in Number Theory, Physics, and Geometry II – On Conformal Field Theories, Discrete Groups and Renormalization. Berlin: Springer-Verlag. 2007: 3–65. ISBN 978-3-540-30307-7. 

外部链接

• 埃里克·韦斯坦因. Polylogarithm. MathWorld. 
• 埃里克·韦斯坦因. Dilogarithm. MathWorld. 
• Algorithms in Analytic Number Theory provides an arbitrary-precision, GMP-based, GPL-licensed implementation.