维基百科:知识问答/存档/2024年10月

三角形三邊邊長呈整數等差數列，且有一內角為120度，求其三邊邊長之比？

三角形三邊邊長皆為整數，且呈等差數列，有一內角為120度，求其三邊邊長之比？---游蛇脫殼/克勞棣 2024年9月29日 (日) 13:40 (UTC)

參照餘弦定理，

餘弦定理：c²=a²+b²-2ab*cosγ

把右圖的(b,a,c,γ)用(a-x, a, a+x, 120°)帶入後可解出2a=5x，x=2/5*a。

然後把上面的結論帶入a-x:a:a+x能得出結果是3:5:7。得解--竹林下小徑，月光映一葉 2024年10月1日 (二) 04:23 (UTC)

按照《1984》书里那个情况，大洋国怎样才能民主化？

按照《1984》书里那个情况，大洋国怎样才能民主化？Wjjksjzs（留言） 2024年10月3日 (四) 14:52 (UTC)

你们分析分析，为什么Microsoft Edge的英译中会把英维的See also模板翻译出了俄文？

帖子我发到了Microsoft Community。模板是这个，我从众多条目中随机挑选了几个做了测试。--Txkk（留言） 2024年9月29日 (日) 06:45 (UTC)

微软Bing翻译服务的问题，See also: …… 到简体中文、繁体中文都如此。页脚的反馈我提报了一下。--YFdyh000（留言） 2024年9月29日 (日) 08:02 (UTC)

还真是这样[1]--Txkk（留言） 2024年9月29日 (日) 08:32 (UTC)

我想知道是哪个关键词触发了错误。--Txkk（留言） 2024年9月29日 (日) 08:39 (UTC)

很难找出。See also: internet in China、See also: internet in US、See also: internet in Beijing、See also: Internet in china等触发，See also: Internet in US等不触发。See also: Intel in China不触发，See also: intel in China触发。--YFdyh000（留言） 2024年9月29日 (日) 09:07 (UTC)

Microsoft Agents让我使用Windows 10/11的“反馈中心”应用向微软发送反馈（见原帖），但我最近暂时没有电脑可用，你可以替我操作吗？--Txkk（留言） 2024年10月4日 (五) 12:07 (UTC)

我没看到合适的反馈分类。他说“我会对该问题进行内部反馈”，我希望这更有用。我再次从翻译器页面的反馈提交了您的帖子，以及从Edge-反馈提交该问题（这也是“反馈中心”推荐的Edge问题反馈方式）。--YFdyh000（留言） 2024年10月4日 (五) 12:35 (UTC)

为什么英语没有自己的管理机构？

像法语有法兰西科学院，加泰罗尼亚语有两个，但英语却没有？--ABCDEAN（留言） 2023年2月11日 (六) 08:47 (UTC)

谁去管？英国还是美国？例如雅思（澳大利亚、英国）和托福（美国）。——Sakamotosan路过围观 | 避免做作，免敬 2024年10月9日 (三) 04:09 (UTC)

「酒駕者、垃圾」與「酒駕者，垃圾」意思有什麼不一樣？

如題。謝謝！---游蛇脫殼/克勞棣 2024年10月10日 (四) 06:17 (UTC)

顿号表示并列词语，“酒驾者、垃圾”即“酒驾者和垃圾”；逗号则是用于停顿，“酒驾者，垃圾”表示对酒驾者的鄙视、批评之意。--自由雨日🌧️（留言｜贡献） 2024年10月10日 (四) 06:20 (UTC)

所以「酒駕者，垃圾」的意思是「酒駕者簡直是垃圾」，是省略繫動詞的隱喻的一種嗎？-游蛇脫殼/克勞棣 2024年10月10日 (四) 06:33 (UTC)

并非省略动词，汉语主谓之间本来就不必须有动词，名词可以直接作谓语。至于“隐喻”（大陆称“暗喻”）的话，我觉得应该是。--自由雨日🌧️（留言｜贡献） 2024年10月10日 (四) 06:36 (UTC)

另外据我所知汉语好像没有“系动词”的说法，“是”属于“判断动词”。--自由雨日🌧️（留言｜贡献） 2024年10月10日 (四) 06:37 (UTC)

好！暫時不管這些文法名詞。請問「酒駕者，垃圾」的意思是不是「酒駕者簡直是垃圾」？-游蛇脫殼/克勞棣 2024年10月10日 (四) 06:55 (UTC)

没有“简直”这层含义啊，“酒驾者是垃圾”比较接近。--自由雨日🌧️（留言｜贡献） 2024年10月10日 (四) 07:10 (UTC)

是略喻。（俗語）女人心，海底針。即女人心是海底針。女人心如海底針。--Shyangs（留言） 2024年10月10日 (四) 08:02 (UTC)

关于广告过滤器与权限限制

为何与维基百科无关？:我认为此问题与与mediawiki的有关而与社区无关。

不懂就问：

为什么我尝试将条目"zh-hk:我的妹妹是黃漫老師"的源代码复制到沙盒内并保存时，

过滤器提示：

"警告：您的编辑行为已被自动过滤器认为是散發廣告及宣傳。请谨记加入推銷性內容可能会导致您的编辑权限遭到剥夺。 如果您確信您沒有進行宣傳，请再次点击“发布更改”。有其他問題可至互助客棧提出。"

如果条目"zh-hk:我的妹妹是黃漫老師"的源代码有"散發廣告及宣傳"的嫌疑，是否应该删除条目"zh-hk:我的妹妹是黃漫老師"？～～～～--209.9.202.205（留言） 2024年10月12日 (六) 17:18 (UTC)

过滤器由社群成员编写，遇到问题请报告至WP:AFFP。——暁月凛奈 (留言) 2024年10月12日 (六) 19:21 (UTC)

擁有120度角的三角形與擁有60度角的三角形的邊長問題

已知某三角形三邊邊長為數組(a,b,c)，其中c的對角為120度，請證明邊長為(a,a+b,c)或(b,a+b,c)的三角形，c的對角為60度。謝謝！---游蛇脫殼/克勞棣 2024年10月10日 (四) 06:26 (UTC)

这真的是个真命题吗？随便举一反例，$a=1,b=1,c={\sqrt {3}}$，此时后面所说的三角形甚至都不存在。况且，后一种“(b,b+c,c)”的三角形明显永远不满足“两边之和大于第三边”。

当然，如果是题目抄错了，解决这个问题的思路也很简单，就是用余弦定理将已知条件表达为三边的关系（比如这里是$c^{2}=a^{2}+b^{2}+ab$），然后同样再用余弦定理计算要求的三角形的$\cos C$的值就好（比如这里就是要证明$\cos C=0.5$）。--_古怪的Wang31（讨论 | 贡献） 2024年10月13日 (日) 01:15 (UTC)

的確抄錯，已修正，謝謝！-游蛇脫殼/克勞棣 2024年10月13日 (日) 14:48 (UTC)

陈竺是中华人民共和国H指数最高的国家领导人吗？

最近试着了解中医、砷制剂和白血病的故事，过程中看到陈竺的复数篇论文，这对于一个国家领导人似乎不多见。考虑到这位做的基础医学算是最常互相引用的领域，他是否是目前中华人民共和国H指数最高的国家领导人？--Trz1118（留言）来人救救金属学和材料科学条目们吧 2024年10月14日 (一) 09:01 (UTC)

他目前不是國家領導人吧？-游蛇脫殼/克勞棣 2024年10月14日 (一) 10:00 (UTC)

肯定是从建国到目前啦……副国级也是国！（其实主要是我当时没意识到他是副委员长，不过这样的话，就将错就错把副国级也算上吧）--Trz1118（留言）来人救救金属学和材料科学条目们吧 2024年10月14日 (一) 10:53 (UTC)

不是「副」算不算的問題，而是根據條目所載，他2023年3月就卸任副委員長了，他目前連「副」都不是了。還是我有所誤會，他目前仍有中華人民共和國的某個官方職務？-游蛇脫殼/克勞棣 2024年10月14日 (一) 12:42 (UTC)

“目前”是“截至目前”，不是“现任的”。--YFdyh000（留言） 2024年10月14日 (一) 15:25 (UTC)

正弦函數的角度與函數值以及等差數列

$0<\theta _{1},\theta _{2},\theta _{3}<\pi$，$k_{1},k_{2},k_{3}$皆為正實數，且

$\sin \theta _{1}={\frac {\sqrt {k_{1}}}{2}}$

$\sin \theta _{2}={\frac {\sqrt {k_{2}}}{2}}$

$\sin \theta _{3}={\frac {\sqrt {k_{3}}}{2}}$

$\theta _{1},\theta _{2},\theta _{3}$呈公差為正的等差數列，$k_{1},k_{2},k_{3}$亦呈公差為正的等差數列，

則請問數組$(\theta _{1},\theta _{2},\theta _{3})$是否只有$({\frac {\pi }{6}},{\frac {\pi }{4}},{\frac {\pi }{3}})$一解？

---游蛇脫殼/克勞棣 2024年10月14日 (一) 21:13 (UTC)

量子纠缠现象属于唯物主义还是唯心主义？

能否有人做一个详细的解释？多谢--■■■■（留言） 2024年10月20日 (日) 12:51 (UTC)

量子纠缠是一个现象，不是意识形态。--自由雨日🌧️（留言｜贡献） 2024年10月20日 (日) 13:05 (UTC)

關於「邊長(a, b, c)的三角形，c的對角是x度； 邊長(a+1 ,b ,c)的三角形，c的對角也是x度」的問題

邊長(a, b, c)的三角形，c的對角是x度

邊長(a+1 ,b ,c)的三角形，c的對角也是x度

例如數組(a,b,c)=(7,15,13)就是滿足上述條件的一組解

請證明(a,b,c)有無限多組整數解。謝謝！---游蛇脫殼/克勞棣 2024年10月13日 (日) 15:02 (UTC)

這題有2種情況，一種是最長邊互相平行不重合，另一種則是最長邊是同一條線。

用後面的情況來講，就像是「全等三角形#SSA配圖中的GF距離為1」的情況。

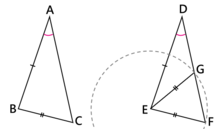
假定此處的DE為最長邊方可適用

所以大概只要找1個3邊長為整數的非正三角形(△DGE)，且其以DG為底的高交於DG延長線上之點距離G或F都是0.5就行了?

要驗證是否符合的話，假定三邊長分別為(a,b,c)，且a<b<c下是否符合c²=a²+a+b² =a(a+1)+b²。

• 以樓主的範例而言，即是15²=7*(7+1)+13² → 225=56+169 這樣
• 對照附圖則是(a,b,c)=(DG,EG,DE)--竹林下小徑，月光映一葉 2024年10月15日 (二) 03:29 (UTC)

所以請問為什麼(a,b,c)有無限多組整數解，而不是有限多組整數解？-游蛇脫殼/克勞棣 2024年10月16日 (三) 09:27 (UTC)

@AromaTake君：我自己找到答案了。

${\begin{cases}a=4t-1\\b=5t-1\\c=3t-1\end{cases}}$ 其中$t$為正整數

滿足上述參數式的(a, b, c)皆為其整數解，由於t有無限多個，故(a, b, c)有無限多組整數解。-游蛇脫殼/克勞棣 2024年10月22日 (二) 16:06 (UTC)