基诺·法诺
外观
| 基诺·法诺(Gino Fano) | |
|---|---|
 | |
| 出生 | 1871年1月5日 义大利曼切华 |
| 逝世 | 1952年11月8日(81岁) 义大利维洛那 |
| 国籍 | 义大利 |
| 知名于 | 法诺猜想 法诺平面 法诺纤维化 法诺曲面 法诺簇 |
| 科学生涯 | |
| 研究领域 | 数学 |
基诺·法诺(Gino Fano,1871年1月5日 - 1952年11月8日)是一位义大利数学家,以有限几何的创始人闻名。法诺生于义大利曼切华,死于义大利维洛那。
法诺为投影几何与代数几何作出许多贡献。他对几何基础的研究比大卫·希尔伯特所做的研究早了十年左右。法诺有两个儿子,名为乌戈·法诺(Ugo Fano)与罗伯特·法诺(Robert Fano)。
法诺是有限投影空间此一领域里的先驱。在他证明 n 维投影空间之公理的独立性[1]与其他定理的文章[2]之中,他认为可推导出有第4个调和点会等于其共轭。这会导出一个具7个点及7条线的配置被包含于一个具15个点、35条线及15个平面的有限三维空间内,其中每条线只包含3个点[2]:114。此一空间内的所有平面均由7个点及7条线所组成,且现在被称之为法诺平面:
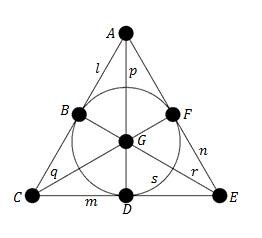
法诺继续描述任意维度与质数阶的有限投影空间。
1907年,法诺为克莱因百科全书贡献了两篇文章。第一篇(SS. 221-88)比较解析几何与综合几何在19世纪的发展。第二篇(SS. 282-388)讲述几何内的连续群及以群论作为几何的统一原则[3]。
注记
[编辑]- ^ Collino, Conte & Verra 2013,p. 6
- ^ 2.0 2.1 Fano, G., Sui postulati fondamentali della geometria proiettiva, Giornale di Matematiche, 1892, 30: 106–132 [2015-08-04], (原始内容存档于2015-07-24)
- ^ Fano, Gino. Kontinuierliche geometrische Gruppen. Die Gruppentheorie als geometrisches Einteilungsprinzip. Encyclopädie der mathematischen Wissenschaften. 1907, 3.1.1: 289–388. doi:10.1007/978-3-663-16027-4_5.
参考文献
[编辑]- Collino, Alberto; Conte, Alberto; Verra, Alessandro. On the life and scientific work of Gino Fano. 2013. arXiv:1311.7177
 .
.
- Grattan-Guinness, Ivor. The Search for Mathematical Roots 1870–1940. Princeton University Press. 2000.
外部链接
[编辑]- 约翰·J·奥康纳; 埃德蒙·F·罗伯逊, Fano, MacTutor数学史档案 (英语)
- 基诺·法诺在数学谱系计画的资料。
