資料加密標準

數據加密標準

DES中的費斯妥函數（F函數）
概述
設計者	IBM
首次發佈	1977（於1979年1月標準化）
衍生自	Lucifer
繼承演算法	Triple DES, G-DES, DES-X, LOKI89, ICE
密碼細節
金鑰長度	56位
分組長度	64位元
結構	平衡費斯妥網絡
重複回數	16
最佳公開破解
由於窮舉法對DES的破解已經成為可能（見暴力破解），DES現在被認為是不安全的。2008年，最佳的分析攻擊是線性密碼分析，要求243個已知明文，具有239–43的時間複雜性；在選擇明文攻擊下，數據複雜性可以減少到其1/4。

數據加密標準（英語：Data Encryption Standard，縮寫為 DES）是一種對稱金鑰加密塊密碼演算法，1976年被美國聯邦政府的國家標準局確定為聯邦資料處理標準（FIPS），隨後在國際上廣泛流傳開來。它基於使用56位金鑰的對稱演算法。這個演算法因為包含一些機密設計元素，相對短的金鑰長度以及懷疑內含美國國家安全域（NSA）的後門而在開始時有爭議，DES因此受到了強烈的學院派式的審查，並以此推動了現代的塊密碼及其密碼分析的發展。

DES現在已經不是一種安全的加密方法，主要因為它使用的56位金鑰過短。1999年1月，distributed.net與電子前哨基金會合作，在22小時15分鐘內即公開破解了一個DES金鑰。也有一些分析報告提出了該演算法的理論上的弱點，雖然在實際中難以應用。為了提供實用所需的安全性，可以使用DES的衍生演算法3DES來進行加密，雖然3DES也存在理論上的攻擊方法。DES標準和3DES標準已逐漸被進階加密標準（AES）所取代。另外，DES已經不再作為國家標準科技協會（前國家標準局）的一個標準。

在某些文獻中，作為演算法的DES被稱為DEA（Data Encryption Algorithm，數據加密演算法），以與作為標準的DES區分開來。在發音時，DES可以作為縮寫按字母拼出來(/ˌdiːˌiːˈɛs/)，或作為一個詞念成/ˈdɛz/。

DES的歷史

DES最初出現在1970年代早期。1972年，在一個對美國政府的電腦安全需求的研究得出結果後，NBS（國家標準局，現在的NIST）開始徵集用於加密政府內非機密敏感資訊的加密標準。因此1973年5月15日，在諮詢了美國國家安全域（NSA）之後，NBS向公眾徵集可以滿足嚴格設計標準的加密演算法。然而，沒有一個提案可以滿足這些要求。因此在，1974年8月27日，NBS開始了第二次徵集。這一次，IBM提交了一種在1973-1974年間發展的演算法，這份提案被有限度的接受了。這種演算法是基於早先霍斯特·費斯妥（Horst Fiestel）提出的Lucifer演算法的。費斯妥，沃爾特·塔克曼（Walter Tuchman），道·科柏密斯（Don Coppersmith），艾倫·康海姆（Alan Konheim），卡爾·梅爾（Carl Meyer），邁克·馬加什（Mike Matyas），羅伊·阿德勒（Roy Adler），埃德娜·格羅斯曼（Edna Grossman），比爾·諾茲（Bill Notz），林恩·史密斯（Lynn Smith）以及布萊恩特·塔克曼等人參與了IBM在演算法設計和分析方面的工作。

美國國家安全域在設計中的作用

1975年3月17日，被選中的DES在「聯邦公報」上公佈並徵集公眾意見。次年，NBS舉行了兩個開放式研討會以討論該標準。不同團體提出了一些意見，其中公開金鑰加密先驅馬丁·赫爾曼和惠特菲爾德·迪菲認為金鑰長度過短以及神奇的「S盒」是NSA的不當干涉的結果。這項論點指出，演算法被情報部門秘密的削弱了，使得他們—而不是別人—可以簡單的讀取加密資訊。S盒的設計者之一，艾倫·康海姆指出：「我們將S盒發給了華盛頓，而他們發回來的S盒變得完全不同了。」因此，美國參議院情報特別委員會審查了NSA的行為以判斷是否存在不當行為。在1978年出版的一份公開的總結中，該委員會寫道：

在DES的開發中，NSA使IBM確信縮短後的金鑰長度也可以滿足需求，間接的幫助了S盒結構的開發，並確認最終的DES演算法可以在他們所知範圍內沒有任何統計學的或數學的弱點。

然而，也有人提到了：

NSA沒有以任何方式干涉演算法的設計。IBM發明和設計了該演算法，做出了一切相關決定，並一致同意金鑰長度超出了所有DES涉及的商業應用的需要。

DES小組的另一個成員，沃爾特·塔克曼說：「完全在IBM內，由我們IBM人，發展了DES演算法。NSA沒有干涉任何設計問題！」相反，一本解密了的NSA關於加密歷史的書則寫道：

1973年NBS向私人工業徵集數據加密標準。第一份投標方案令人失望，因此NSA開始研究它自己的演算法。此後，負責研究和工程的主任霍華德·羅森布拉姆（Howard Rosenblum）發現IBM的沃爾特·塔克曼正在研究修改Lucifer以適應一般應用。NSA為塔克曼發放了一份許可，讓他與情報部門一起研究Lucifer的改進方案。

以及：

NSA與IBM緊密合作以增強演算法針對除了暴力破解以外的攻擊方式，並增強被稱為S盒的置換表的強度。同時，很矛盾的，NSA試圖說服IBM將金鑰長度從64位元削減到48位元，而最終他們達成了妥協，使用56位的金鑰長度。

由於艾力·畢漢姆（Eli Biham）和阿迪·薩莫爾（Adi Shamir）獨立發現和公開了差分密碼分析，一種破解塊密碼的通用方法，針對S盒中隱藏的弱點的懷疑在1990年平靜了下來。DES的S盒的設計使得該演算法對這種攻擊方法的抵抗能力大大強於隨機的S盒，該事實強烈的支援了IBM在1970年代就已經知道了其中的技術背景的說法。這的確是事實—1994年，科柏密斯公開了一些原創的S盒的設計準則。據史蒂文·列維（Steven Levy）說，IBM的華生研究院（Watson）在1974年發現了差分密碼攻擊，而NSA要求保持技術秘密。科柏密斯解釋IBM的保密決定說：「那是因為差分密碼攻擊是一種強有力的針對許多演算法的工具，因此有人認為公開這樣的資訊可能對國家安全產生不利影響。」列維參照沃爾特·塔克曼的話說：「他們讓我們將我們所有的檔案可靠的封存起來...我們的確對每一份檔案進行編號，並將它們放在保險箱裏，因為這些檔案被認為是美國政府機密。他們說這樣做，所以我照做了。」

作為標準的演算法

雖然仍有一些批評，DES在1976年11月被確定為聯邦標準，並在1977年1月15日作為FIPS PUB 46發佈，被授權用於所有非機密資料。它在1988年（修訂為FIPS-46-1），1993年（FIPS-46-2）和1999年（FIPS-46-3），後者被規定為3DES（見下文）。2002年5月26日，DES終於在公開競爭中被進階加密標準（AES）所取代。2005年5月26日，FIPS 46-3被官方的拒絕了，但NIST確認3DES在2030年以前均可用於敏感政府資訊的加密。

DES演算法也定義在了ANSI X3.92，以及ISO/IEC 18033-3中（作為TDEA的一部分）。

1994年發表了另一種理論攻擊方法，線性密碼分析，但1998年的一次蠻力攻擊顯示DES可以被實用的破解，顯示了替代演算法的迫切需求。晚些時候的文章更詳細的探討了這些密碼分析的方法。

DES的匯入被認為是密碼學的學術研究的催化劑，尤其是對塊密碼的密碼分析。NIST對DES的回顧中提到：

DES可以被稱為對加密演算法的非軍用研究和發展的開始。1970年代除了為軍隊或情報組織工作的以外，只有很少的密碼學者，對密碼學的學術研究也很少。現在則有許多活躍的學術性的密碼學者，善於密碼學方面編程的數學部分，以及商業資訊保安公司和顧問。一整代的密碼學者都拼命分析（或者說，破解）DES演算法。用密碼學家布魯斯·施奈爾的話說：「DES在促進密碼學界的發展上做的比其它的一切都多。現在有一種演算法供學者們分析了。」在1970和1980年代，密碼學中關於DES的公開文獻所佔的比例令人大吃一驚，而且DES是用來對每一種對稱金鑰演算法進行比較的標準對象。

年代簡表

日期	年份	事件
5月15日	1973	NBS第一次徵集加密演算法標準
8月27日	1974	NBS第二次徵集加密演算法標準
3月17日	1975	DES在「聯邦公報」上發佈並徵集意見
8月	1976	DES的第一次研討會
9月	1976	第二次研討會，討論DES的數學基礎
11月	1976	DES被確認為標準
1月15日	1977	DES被作為FIPS標準FIPS PUB 46發佈
	1983	DES第一次延長標準期限
	1986	HBO開始使用一個基於DES的電視衛星加密系統，Videocipher II
1月22日	1988	DES第二次延長標準期限，稱為FIPS 46-1，取代FIPS PUB 46
7月	1990	畢漢姆和薩莫爾重新發現了差分密碼分析，並將之應用到了一個15位的類DES密碼系統
	1992	畢漢姆和薩莫爾發佈了第一個複雜性小於暴力破解的理論攻擊方法：差分密碼分析。然而，這種方法仍然需要不現實的247選擇明文。
12月30日	1993	DES作為FIPS 46-2第三次延長標準期限
	1994	試驗了第一個實驗性的DES密碼分析，線性密碼分析
6月	1997	DESCHAL計劃第一次公開破解了DES加密的資訊
7月	1998	EFF的DES破解機（Deep Crack）在56小時內破解了DES金鑰
1月	1999	Deep Crack和distributed.net合作在22小時15分鐘內破解了一個DES金鑰
10月25日	1999	DES作為FIPS46-3第四次延長標準期限，其中規定優先使用3DES，而普通DES只允許在遺留的系統中應用
11月26日	2001	AES作為FIPS 197發佈
5月26日	2002	AES標準開始生效
7月26日	2004	「聯邦公報」發佈了FIPS 46-3以及一系列相關標準被駁回的資訊
5月19日	2005	NIST拒絕了FIPS 46-3標準
4月	2006	德國魯爾大學和基爾大學基於FPGA的價值$10,000的平行計算機COPACOBANA在9天內破解了DES在一年內，軟件改進將平均時間降低到了6.4天。
11月	2008	COPACOBANA的下一代，RIVYERA將平均破解時間降低到了一天內

替代演算法

安全性方面的考慮使得研究者在1980年代晚期和1990年代早期提出了一系列替代的塊密碼設計，包括RC5，Blowfish，IDEA，NewDES，SAFER，CAST5和FEAL。這些設計的大多數保持了DES的64位元的塊大小，可以作為DES的直接替代方案，雖然這些方案通常使用64位元或128位元的金鑰。蘇聯匯入了GOST 28147-89演算法，該演算法的塊大小為64位元，而金鑰長度為256位，並在晚些時候的俄羅斯得到了應用。

2000年代，DES逐漸被3DES替代。3DES相當於用兩個（2TDES）或三個（3TDES）不同的金鑰對數據進行三次DES加密。2010年代，3DES逐漸被更安全的高級加密標準（AES）替代。

2000年10月，在歷時接近5年的徵集和選拔之後，NIST選擇了進階加密標準（AES）替代DES和3DES。2001年2月28日，聯邦公報發表了AES標準，以此開始了其標準化行程，並於2001年11月26日成為FIPS PUB 197標準。AES演算法在提交的時候稱為Rijndael。選拔中其它進入決賽的演算法包括RC6，Serpent，MARS和Twofish。

演算法描述

圖1—DES中的總體費斯妥結構

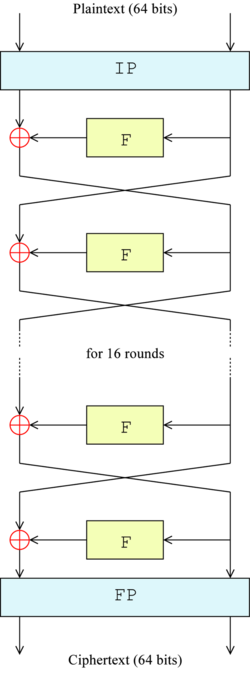
為簡明起見，下文中的敘述省略的各變換和置換的細節，可以在DES補充材料中找到對應的尋找表。

DES是一種典型的塊密碼—一種將固定長度的明文通過一系列複雜的操作變成同樣長度的密文的演算法。對DES而言，塊長度為64位元。同時，DES使用金鑰來自訂變換過程，因此演算法認為只有持有加密所用的金鑰的用戶才能解密密文。金鑰表面上是64位元的，然而只有其中的56位被實際用於演算法，其餘8位元可以被用於奇偶校驗，並在演算法中被丟棄。因此，DES的有效金鑰長度僅為56位。

與其它塊密碼相似，DES單單它自身並不構成加密的實用手段，而必須以某種工作模式進行實際操作。FIPS-81確定了DES使用的幾種模式。FIPS-74包括了更多關於DES使用的討論。

整體結構

演算法的整體結構如圖1所示：有16個相同的處理過程，稱為「回次」（round），並在首尾各有一次置換，稱為IP與FP（或稱IP^-1，FP為IP的反函數（即IP「復原」FP的操作，反之亦然）。IP和FP幾乎沒有密碼學上的重要性，為了在1970年代中期的硬件上簡化輸入輸出資料庫的過程而被顯式的包括在標準中。

在主處理回次前，數據塊被分成兩個32位元的半塊，並被分別處理；這種交叉的方式被稱為費斯妥結構。費斯妥結構保證了加密和解密過程足夠相似—唯一的區別在於子金鑰在解密時是以反向的順序應用的，而剩餘部分均相同。這樣的設計大大簡化了演算法的實現，尤其是硬件實現，因為沒有區分加密和解密演算法的需要。

圖中的⊕符號代表異或（XOR）操作。「F函數」將數據半塊與某個子金鑰進行處理。然後，一個F函數的輸出與另一個半塊異或之後，再與原本的半塊組合併交換順序，進入下一個回次的處理。在最後一個回次完成時，兩個半塊需要交換順序，這是費斯妥結構的一個特點，以保證加解密的過程相似。

費斯妥函數（F函數）

圖2中顯示了費斯妥函數（F函數）的過程。其每次對半塊（32位元）進行操作，並包括四個步驟：

圖2—DES的費斯妥函數（F函數）

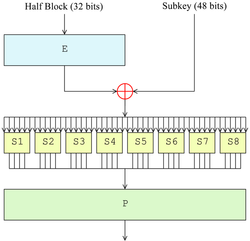
1. 擴張—用擴張置換（圖中的E）將32位元的半塊擴充到48位元，其輸出包括8個6位的塊，每塊包含4位元對應的輸入位，加上兩個鄰接的塊中緊鄰的位。
2. 與金鑰混合—用異或操作將擴張的結果和一個子金鑰進行混合。16個48位元的子金鑰—每個用於一個回次的F變換—是利用金鑰排程從主金鑰生成的（見下文）。
3. S盒—在與子金鑰混合之後，塊被分成8個6位的塊，然後使用「S盒」，或稱「置換盒」進行處理。8個S盒的每一個都使用以尋找表方式提供的非線性的變換將它的6個輸入位變成4個輸出位。S盒提供了DES的核心安全性—如果沒有S盒，密碼會是線性的，很容易破解。
4. 置換—最後，S盒的32個輸出位利用固定的置換，「P置換」進行重組。這個設計是為了將每個S盒的4位元輸出在下一回次的擴張後，使用4個不同的S盒進行處理。

S盒，P置換和E擴張各自滿足了克勞德·香農在1940年代提出的實用密碼所需的必要條件，「混淆與擴散」。

金鑰排程

圖3—DES的金鑰排程

圖3顯示了加密過程中的金鑰排程—產生子金鑰的演算法。首先，使用選擇置換1（PC-1）從64位元輸入金鑰中選出56位的金鑰—剩下的8位元要麼直接丟棄，要麼作為奇偶校驗位。然後，56位分成兩個28位元的半金鑰；每個半金鑰接下來都被分別處理。在接下來的回次中，兩個半金鑰都被左移1或2位（由回次數決定），然後通過選擇置換2（PC-2）產生48位元的子金鑰—每個半金鑰24位元。移位（圖中由<<標示）表明每個子金鑰中使用了不同的位，每個位大致在16個子金鑰中的14個出現。

解密過程中，除了子金鑰輸出的順序相反外，金鑰排程的過程與加密完全相同。

安全與密碼分析

雖然已發表的針對DES的密碼分析的研究文章多於所有其它的塊密碼，到目前為止，最實用的攻擊方法仍然是暴力攻擊。已知DES有一些次要的可能導致加密強度降低的密碼學特性，同時有3種理論攻擊的理論複雜性小於暴力破解，但由於需要過於龐大而通常不現實的已知明文或選擇明文數量，故實用價值微乎其微。

暴力破解

主條目：DES破解機

對於一切密碼而言，最基本的攻擊方法是暴力破解法—依次嘗試所有可能的金鑰。金鑰長度決定了可能的金鑰數量，因此也決定了這種方法的可行性。對於DES，即使在它成為標準之前就有一些關於其金鑰長度的適當性的問題，而且也正是它的金鑰長度，而不是理論密碼分析迫使它被後續演算法所替代。在設計時，在與包括NSA在內的外部顧問討論後，金鑰長度被從128位元減少到了56位以適應在單晶片上實現演算法。

EFF的價值250,000美元的DES破解機包括1,856個自訂的晶片，可以在數天內破解一個DES金鑰—本圖顯示了使用數個Deep Crack晶片搭成的DES破解機

在學術上，曾有數個DES破解機被提出。1977年，迪菲和海爾曼提出了一部造價約2千萬美元的破解機，可以在一天內找到一個DES金鑰。1993年，米高·維納設計了一部造價約1百萬美元的破解機，大約可以在7小時內找到一個金鑰。然而，這些早期的設計並沒有被實現，至少沒有公開的實現。在1990年代晚期，DES開始受到實用的攻擊。1997年，RSA安全贊助了一系列的競賽，獎勵第一個成功破解以DES加密的資訊的隊伍1萬美元，洛克·韋爾謝什（Rocke Verser），馬特·柯廷（Matt Curtin）和賈斯廷·多爾斯基（Justin Dolske）領導的DESCHALL計劃獲勝，該計劃使用了數千台連接到互聯網的電腦的閒置計算能力。1998年，電子前哨基金會（EFF，一個資訊人權組織）製造了一台DES破解機，造價約$250,000。該破解機可以用稍多於2天的時間暴力破解一個金鑰，它顯示了迅速破解DES的可能性。EFF的動力來自於向大眾顯示DES不僅在理論上，也在實用上是可破解的：

許多人在親眼見到一個事實前不會相信它。向他們顯示一台實際的機器可以在數天內破解DES是讓某些人相信他們不能依賴DES的安全性的唯一方法。

下一個確認的DES破解機是2006年由德國的魯爾大學與基爾大學的工作群組建造的COPACOBANA。與EFF的不同，COPACOBANA由商業上可獲得的，可重組態的FPGA組成。120片並列的XILINX Spartan3-1000型FPGA分為20個DIMM模組，每個模組包括6個FPGA。使用可重組態的FPGA使得這種裝置也可以用於其它密碼的破解。另外一個關於COPACOBANA的有趣事實是它的成本。一台COPACOBANA的造價大約是$10,000，是EFF裝置的25分之一，這充分說明了數字電路的持續進步。考慮到通貨膨脹因素，同樣價格的裝置的效能在8年間大約提到了30倍。2007年，COPACOBANA的兩個專案參與者組建的SciEngines公司改進了COPACOBANA，並發展了它的下一代。2008年，他們的COPACOBANA RIVYERA將破解DES的時間減少到了1天以內，使用128片Spartan-3 5000型FPGA。目前SciEngines的RIVYEAR保持着使用暴力破解法破解DES的紀錄。

快於暴力攻擊的攻擊方法

有三種已知方法可以以小於暴力破解的複雜性破解DES的全部16回次：差分密碼分析（DC），線性密碼分析（LC），以及戴維斯攻擊。然而，這些攻擊都是理論性的，難以用於實踐；它們有時被歸結於認證的弱點。

• 差分密碼分析在1980年代晚期由艾力·畢漢姆和阿迪·薩莫爾重新發現；1970年代IBM和NSA便發現了這種方法，但沒有公開。為了破解全部16回次，差分密碼分析需要2⁴⁷組選擇明文。DES被設計為對DC具有抵抗性。

• 線性密碼分析由松井充（Mitsuru Matsui）發現，需要2⁴³組已知明文；該方法已被實現，是第一種公開的實驗性的針對DES的密碼分析。沒有證據顯示DES的設計可以抵抗這種攻擊方法。一般概念上的LC—「多線性密碼分析」—在1994年由Kaliski和Robshaw所建議，並由比留科夫等人於2004年所改進。線性密碼分析的選擇明文變種是一種類似的減少數據複雜性的方法。帕斯卡爾·朱諾德（Pascal Junod）在2001年進行了一些確定線性密碼分析的實際時間複雜性的實驗，結果顯示它比預期的要快，需要約2³⁹–2⁴¹次操作。

• 改進的戴維斯攻擊：線性和差分密碼分析是針對很多演算法的通用技術，而戴維斯攻擊是一種針對DES的特別技術，在1980年代由唐納德·戴維斯（Donald Davies）首先提出，並於1997年為畢漢姆和亞歷克斯·比留科夫（Alex Biryukov）所改進。其最有效的攻擊形式需要2⁵⁰已知明文，計算複雜性亦為2⁵⁰，成功率為51%。

也有一些其它的針對削減了回次的密碼版本，即少於16回次的DES版本。這些攻擊顯示了多少回次是安全所需的，以及完整版本擁有多少「安全餘量」。差分線性密碼分析於1994年為蘭福德（Langford）和海爾曼所提出，是一種組合了差分和線性密碼分析的方法。一種增強的差分線性密碼分析版本可以利用2^15.8組已知明文可以以2^29.2的時間複雜性破解9回次的DES。

次要的密碼學特性

DES有補數特性，即

$E_{K}(P)=C\Leftrightarrow E_{\overline {K}}({\overline {P}})={\overline {C}}$其中${\overline {x}}$是$x$的補數，$E_{K}$是以$K$為金鑰的加密函數，$P$和$C$分別表示明文和密文。這樣的性質表明暴力破解的工作量在選擇明文攻擊下可以減少一半。

DES有四個所謂的弱金鑰。若使用弱金鑰，加密和解密有相同的效果（參見對合)：

$E_{K}(E_{K}(P))=P$或$E_{K}=D_{K}$

也有6對半弱金鑰。若使用某個半弱金鑰$K_{1}$進行加密，則相當於使用其對應的半弱金鑰$K_{2}$進行解密：

$E_{K_{1}}(E_{K_{2}}(P))=P$或，$E_{K_{2}}=D_{K_{1}}$

在實現中可以輕易的避開弱金鑰和半弱金鑰，可以顯式的測試金鑰，或簡單的隨機選擇金鑰：剛好選到弱或半弱金鑰的可能性幾乎沒有。這些金鑰事實上並不比其它的金鑰弱，因為他們沒有給攻擊以任何可利用的好處。

DES也被證明不是群，或更精確的，集合$\{E_{K}\}$（對於所有可能的金鑰$K$）在複合函數之下不是一個群，也不「近似」於一個群。這有時是一個開放式的問題，而且若是這種情況，破解DES是可能的，且類似於3DES的加密模式不能增加其安全性。

DES的最大密碼學安全性被限制在了約64位元，除非獨立選擇每個回次的子金鑰而不是從金鑰中生成，這樣做可以將允許768位元的安全性。

參考文獻

來源

• Ehrsam 等：《用於數據安全的塊密碼系統產品》, 美國專利第3,962,539號, 1975年2月24日發佈
• Gilmore, John. 《破解DES：加密研究的秘密，竊聽政策和晶片設計》, 1998, O'Reilly, ISBN 978-1-56592-520-5

外部連結

• EFF的DES破解器計劃
• 針對DES的密碼學提示
• John Savard對DES的描述DES
• 可以顯示中間值的基於Javascript的DES計數機 （頁面存檔備份，存於互聯網檔案館）
• COPACOBANA，魯爾大學和基爾大學的基於FPGA的價值$10,000的DES破解器
• RFC4772 :使用DES的安全隱患 （頁面存檔備份，存於互聯網檔案館）
• 一份簡單的DES/3DES實現文件 （頁面存檔備份，存於互聯網檔案館）

參見

• 金鑰密碼學
• Skipjack加密
• 布萊恩特·塔克曼
• 3DES