本条目中,矢量 与标量 分别用粗体 与斜体 显示。例如,位置矢量通常用
r
{\displaystyle \mathbf {r} \,\!}
r
{\displaystyle r\,\!}
在静电学 里,电势能 (electric potential energy )是处于电场 的电荷 分布所具有的势能 ,与电荷分布在系统内部的组态有关。电势能的单位是焦耳 。电势能与电势 不同。电势定义为处于电场的电荷所具有的电势能每单位电荷 。电势的单位是伏特 。
电势能的数值不具有绝对意义,只具有相对意义。所以,必须先设定一个电势能为零的参考系统。当物理系统内的每一个点电荷相距无穷远且其相对静止不动时,这一物理系统通常可以设定为电势能等于零的参考系统。[ 1] :§25-1 假设一个物理系统里的每一个点电荷,从无穷远处被一外力匀速地迁移到其所在位置,该外力做的总机械功 为
W
{\displaystyle W}
U
{\displaystyle U}
U
:=
W
{\displaystyle U:=W}
在这过程里,所涉及的机械功
W
{\displaystyle W}
如此计算电势能,并没有考虑到移动的路径,这是因为电场是保守场 ,电势能只跟初始位置与终止位置有关,与路径无关。
在一个物理系统内,计算一个点电荷所具有的电势能的方法,就是计算将这点电荷Q从无穷远位置迁移到其它固定位置电荷附近所需要做的机械功。而计算只需要两个参数:
其它电荷所产生的电势。
点电荷Q的电荷量。 注意:这里的计算不需要知道其它电荷的电荷量,也不需要知道这一点电荷Q所产生的电势。
只拥有单独一个点电荷的物理系统,其电势能为零,因为没有任何其它可以产生电场的源电荷,所以,将点电荷从无穷远移动至其最终位置,外机制不需要对它做任何机械功。特别注意,这点电荷有可能会与自己生成的电场发生作用。然而,由于在点电荷的位置,它自己生成的电场为无穷大,所以,在计算系统的有限总电势能之时,一般刻意不将这“自身能”纳入考量范围之内,以简化物理模型,方便计算。
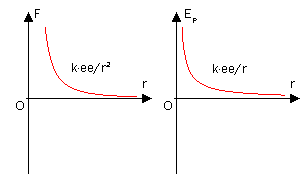
一个质子受到的另一个质子的电场力和电势能随
r
{\displaystyle r}
思考两个点电荷所组成的物理系统。假设第一个点电荷
q
1
{\displaystyle q_{1}}
原点
O
{\displaystyle \mathbf {O} }
库仑定律 ,点电荷
q
1
{\displaystyle q_{1}}
r
{\displaystyle \mathbf {r} }
q
2
{\displaystyle q_{2}}
电场力 为
F
c
=
q
1
q
2
4
π
ϵ
0
r
^
r
2
{\displaystyle \mathbf {F} _{c}={\frac {q_{1}q_{2}}{4\pi \epsilon _{0}}}\ {\frac {\hat {\mathbf {r} }}{r^{2}}}}
其中,
ϵ
0
{\displaystyle \epsilon _{0}}
电常数 。
在移动点电荷
q
2
{\displaystyle q_{2}}
−
F
c
{\displaystyle -\mathbf {F} _{c}}
q
2
{\displaystyle q_{2}}
W
{\displaystyle W}
W
=
−
∫
L
F
c
⋅
d
ℓ
=
−
q
1
q
2
4
π
ϵ
0
∫
L
r
^
r
2
⋅
d
ℓ
{\displaystyle W=-\int _{\mathbb {L} }\mathbf {F} _{c}\cdot \mathrm {d} {\boldsymbol {\ell }}=-\ {\frac {q_{1}q_{2}}{4\pi \epsilon _{0}}}\int _{\mathbb {L} }{\frac {\hat {\mathbf {r} }}{r^{2}}}\cdot \mathrm {d} {\boldsymbol {\ell }}}
由于库仑力为保守力 ,机械功与积分路径
L
{\displaystyle \mathbb {L} }
−
r
^
{\displaystyle -{\hat {\mathbf {r} }}}
r
{\displaystyle \mathbf {r} }
W
=
−
q
1
q
2
4
π
ϵ
0
∫
∞
r
d
r
r
2
=
q
1
q
2
4
π
ϵ
0
r
{\displaystyle W=-\ {\frac {q_{1}q_{2}}{4\pi \epsilon _{0}}}\int _{\infty }^{r}{\frac {\mathrm {d} r}{r^{2}}}={\frac {q_{1}q_{2}}{4\pi \epsilon _{0}r}}}
这机械功是无穷远位置与
r
{\displaystyle \mathbf {r} }
W
=
U
(
r
)
−
U
(
∞
)
{\displaystyle W=U(\mathbf {r} )-U(\infty )}
设定
U
(
∞
)
=
0
{\displaystyle U(\infty )=0}
U
(
r
)
=
q
1
q
2
4
π
ϵ
0
r
{\displaystyle U(\mathbf {r} )={\frac {q_{1}q_{2}}{4\pi \epsilon _{0}r}}}
现在,假设两个点电荷的位置分别为
r
1
{\displaystyle \mathbf {r} _{1}}
r
2
{\displaystyle \mathbf {r} _{2}}
U
=
1
4
π
ϵ
0
q
1
q
2
|
r
2
−
r
1
|
=
1
4
π
ϵ
0
q
1
q
2
r
12
{\displaystyle U={\frac {1}{4\pi \epsilon _{0}}}\ {\frac {q_{1}q_{2}}{|\mathbf {r} _{2}-\mathbf {r} _{1}|}}={\frac {1}{4\pi \epsilon _{0}}}\ {\frac {q_{1}q_{2}}{r_{12}}}}
其中,
r
12
=
|
r
2
−
r
1
|
{\displaystyle r_{12}=|\mathbf {r} _{2}-\mathbf {r} _{1}|}
假设两个点电荷的正负性相异,则电势能为负值,两个点电荷会互相吸引;否则,电势能为正值,两个点电荷会互相排斥。
对于三个点电荷的系统,外机制将其每一个单独点电荷,一个接着一个,从无穷远位置迁移至最终位置,所需要做的机械功,就是整个系统的静势能。以方程表示,
U
=
1
4
π
ϵ
0
(
q
1
q
2
r
12
+
q
1
q
3
r
13
+
q
2
q
3
r
23
)
{\displaystyle U={\frac {1}{4\pi \epsilon _{0}}}\left({\frac {q_{1}q_{2}}{r_{12}}}+{\frac {q_{1}q_{3}}{r_{13}}}+{\frac {q_{2}q_{3}}{r_{23}}}\right)}
其中,
q
1
,
q
2
,
q
3
{\displaystyle q_{1},q_{2},q_{3}}
r
i
j
{\displaystyle r_{ij}}
按照这方法演算,对于多个点电荷的系统,按照顺序,从第一个点电荷到最后一个点电荷,各自移动到最后对应位置。在第
i
{\displaystyle i}
q
i
{\displaystyle q_{i}}
1
{\displaystyle 1}
i
−
1
{\displaystyle i-1}
W
i
{\displaystyle W_{i}}
W
i
=
1
4
π
ϵ
0
∑
j
=
1
i
−
1
q
i
q
j
r
i
j
{\displaystyle W_{i}={\frac {1}{4\pi \epsilon _{0}}}\sum _{j=1}^{i-1}{\frac {q_{i}q_{j}}{r_{ij}}}}
所有点电荷做出的总机械功(即总电势能)为[ 2]
U
=
W
=
∑
i
=
1
n
W
i
=
1
4
π
ϵ
0
∑
i
=
1
n
∑
j
=
1
i
−
1
q
i
q
j
r
i
j
{\displaystyle U=W=\sum _{i=1}^{n}W_{i}={\frac {1}{4\pi \epsilon _{0}}}\sum _{i=1}^{n}\sum _{j=1}^{i-1}{\frac {q_{i}q_{j}}{r_{ij}}}}
将每一个项目重复多计算一次,然后将总和除以
2
{\displaystyle 2}
U
=
1
8
π
ϵ
0
∑
i
=
1
n
∑
j
=
1
,
j
≠
i
n
q
i
q
j
r
i
j
{\displaystyle U={\frac {1}{8\pi \epsilon _{0}}}\sum _{i=1}^{n}\sum _{j=1,j\neq i}^{n}{\frac {q_{i}q_{j}}{r_{ij}}}}
这样,可以忽略点电荷的迁移顺序。
注意到除了点电荷
q
i
{\displaystyle q_{i}}
r
i
{\displaystyle \mathbf {r} _{i}}
ϕ
(
r
i
)
=
1
4
π
ϵ
0
∑
j
=
1
,
j
≠
i
n
q
j
r
i
j
{\displaystyle \phi (\mathbf {r} _{i})={\frac {1}{4\pi \epsilon _{0}}}\sum _{j=1,j\neq i}^{n}{\frac {q_{j}}{r_{ij}}}}
所以,离散点电荷系统的总电势能为
U
=
1
2
∑
i
=
1
n
q
i
ϕ
(
r
i
)
{\displaystyle U={\frac {1}{2}}\sum _{i=1}^{n}q_{i}\phi (\mathbf {r} _{i})}
上述方程假设电介质是自由空间 ,其电容率 为
ϵ
0
{\displaystyle \epsilon _{0}}
ϵ
{\displaystyle \epsilon }
ϵ
0
{\displaystyle \epsilon _{0}}
ϵ
{\displaystyle \epsilon }
对于连续电荷分布,前面的电势能方程变为[ 2]
U
=
1
2
∫
V
ρ
(
r
)
ϕ
(
r
)
d
3
r
{\displaystyle U={\frac {1}{2}}\int _{\mathbb {V} }\rho (\mathbf {r} )\phi (\mathbf {r} )\ \mathrm {d} ^{3}r}
其中,
ρ
(
r
)
{\displaystyle \rho (\mathbf {r} )}
r
{\displaystyle \mathbf {r} }
电荷密度 ,
V
{\displaystyle \mathbb {V} }
应用高斯定律
∇
⋅
E
=
ρ
ϵ
0
{\displaystyle \mathbf {\nabla } \cdot \mathbf {E} ={\frac {\rho }{\epsilon _{0}}}}
其中,
E
{\displaystyle \mathbf {E} }
电势能为
U
=
ϵ
0
2
∫
V
[
∇
⋅
E
(
r
)
]
ϕ
(
r
)
d
3
r
=
ϵ
0
2
∫
V
∇
⋅
[
E
(
r
)
ϕ
(
r
)
]
−
E
(
r
)
⋅
∇
ϕ
(
r
)
d
3
r
{\displaystyle {\begin{aligned}U&={\frac {\epsilon _{0}}{2}}\int _{\mathbb {V} }[\mathbf {\nabla } \cdot \mathbf {E} (\mathbf {r} )]\phi (\mathbf {r} )\ \mathrm {d} ^{3}r\\&={\frac {\epsilon _{0}}{2}}\int _{\mathbb {V} }\mathbf {\nabla } \cdot [\mathbf {E} (\mathbf {r} )\phi (\mathbf {r} )]-\mathbf {E} (\mathbf {r} )\cdot \mathbf {\nabla } \phi (\mathbf {r} )\ \mathrm {d} ^{3}r\\\end{aligned}}}
。 应用散度定理 ,可以得到
U
=
ϵ
0
2
∮
S
[
E
(
r
)
ϕ
(
r
)
]
⋅
d
2
r
−
ϵ
0
2
∫
V
E
(
r
)
⋅
∇
ϕ
(
r
)
d
3
r
{\displaystyle U={\frac {\epsilon _{0}}{2}}\oint _{\mathbb {S} }[\mathbf {E} (\mathbf {r} )\phi (\mathbf {r} )]\cdot \mathrm {d} ^{2}r-{\frac {\epsilon _{0}}{2}}\int _{\mathbb {V} }\mathbf {E} (\mathbf {r} )\cdot \mathbf {\nabla } \phi (\mathbf {r} )\ \mathrm {d} ^{3}r}
其中,
S
{\displaystyle \mathbb {S} }
V
{\displaystyle \mathbb {V} }
当积分体积
V
{\displaystyle \mathbb {V} }
S
{\displaystyle \mathbb {S} }
r
2
{\displaystyle r^{2}}
1
/
r
2
{\displaystyle 1/r^{2}}
1
/
r
{\displaystyle 1/r}
U
=
−
ϵ
0
2
∫
A
L
L
S
P
A
C
E
E
(
r
)
⋅
∇
ϕ
(
r
)
d
3
r
{\displaystyle U=-{\frac {\epsilon _{0}}{2}}\int _{\mathbb {ALL\ SPACE} }\mathbf {E} (\mathbf {r} )\cdot \mathbf {\nabla } \phi (\mathbf {r} )\mathrm {d} ^{3}r}
电场与电势的微分关系为
E
=
−
∇
ϕ
{\displaystyle \mathbf {E} =-\nabla \phi }
将这方程代入,电势能变为
U
=
ϵ
0
2
∫
A
L
L
S
P
A
C
E
[
E
(
r
)
]
2
d
3
r
{\displaystyle U={\frac {\epsilon _{0}}{2}}\int _{\mathbb {ALL\ SPACE} }[E(\mathbf {r} )]^{2}\mathrm {d} ^{3}r}
所以,电势能密度
u
{\displaystyle u}
u
(
r
)
=
ϵ
0
2
[
E
(
r
)
]
2
{\displaystyle u(\mathbf {r} )={\frac {\epsilon _{0}}{2}}[E(\mathbf {r} )]^{2}}
前面分别推导出两个电势能方程:
U
=
1
8
π
ϵ
0
∑
i
=
1
n
∑
j
=
1
,
j
≠
i
n
q
i
q
j
r
i
j
{\displaystyle U={\frac {1}{8\pi \epsilon _{0}}}\sum _{i=1}^{n}\sum _{j=1,j\neq i}^{n}{\frac {q_{i}q_{j}}{r_{ij}}}}
U
=
ϵ
0
2
∫
A
L
L
S
P
A
C
E
[
E
(
r
)
]
2
d
3
r
{\displaystyle U={\frac {\epsilon _{0}}{2}}\int _{\mathbb {ALL\ SPACE} }[E(\mathbf {r} )]^{2}\mathrm {d} ^{3}r}
注意到第一个方程计算得到的电势能,可以是正值,也可以是负值;但从第一个方程推导出来的第二个方程,其计算得到的电势能则必定是正值。为什么会发生这不一致问题?原因是第一个方程只囊括了电荷与电荷之间的相互作用能;而第二个方程在推导过程中,无可避免地将电荷的自身能也包括在内。在推导第一个方程时,在位置
r
i
{\displaystyle \mathbf {r} _{i}}
q
i
{\displaystyle q_{i}}
举一个双点电荷案例,假设电荷
q
1
{\displaystyle q_{1}}
q
2
{\displaystyle q_{2}}
r
1
{\displaystyle \mathbf {r} _{1}}
r
2
{\displaystyle \mathbf {r} _{2}}
r
{\displaystyle \mathbf {r} }
[ 2]
E
=
E
1
+
E
2
=
q
1
4
π
ϵ
0
r
−
r
1
|
r
−
r
1
|
3
+
q
2
4
π
ϵ
0
r
−
r
2
|
r
−
r
2
|
3
{\displaystyle \mathbf {E} =\mathbf {E} _{1}+\mathbf {E} _{2}={\frac {q_{1}}{4\pi \epsilon _{0}}}\ {\frac {\mathbf {r} -\mathbf {r} _{1}}{|\mathbf {r} -\mathbf {r} _{1}|^{3}}}+{\frac {q_{2}}{4\pi \epsilon _{0}}}\ {\frac {\mathbf {r} -\mathbf {r} _{2}}{|\mathbf {r} -\mathbf {r} _{2}|^{3}}}}
其电势能密度为
u
=
ϵ
0
2
E
2
=
ϵ
0
2
(
E
1
2
+
E
2
2
+
2
E
1
⋅
E
2
)
{\displaystyle u={\frac {\epsilon _{0}}{2}}E^{2}={\frac {\epsilon _{0}}{2}}(E_{1}\,^{2}+E_{2}\,^{2}+2\mathbf {E} _{1}\cdot \mathbf {E} _{2})}
很明显地,这方程右手边的前两个项目分别为电荷
q
1
{\displaystyle q_{1}}
q
2
{\displaystyle q_{2}}
ϵ
0
E
1
2
/
2
{\displaystyle \epsilon _{0}E_{1}\,^{2}/2}
ϵ
0
E
2
2
/
2
{\displaystyle \epsilon _{0}E_{2}\,^{2}/2}
U
i
n
t
=
∫
V
u
i
n
t
d
3
r
=
ϵ
0
∫
V
E
1
⋅
E
2
d
3
r
=
q
1
q
2
16
π
2
ϵ
0
∫
V
r
−
r
1
|
r
−
r
1
|
3
⋅
r
−
r
2
|
r
−
r
2
|
3
d
3
r
{\displaystyle U_{int}=\int _{\mathbb {V} }u_{int}\ \mathrm {d} ^{3}r=\epsilon _{0}\int _{\mathbb {V} }\mathbf {E} _{1}\cdot \mathbf {E} _{2}\ \mathrm {d} ^{3}r={\frac {q_{1}q_{2}}{16\pi ^{2}\epsilon _{0}}}\int _{\mathbb {V} }{\frac {\mathbf {r} -\mathbf {r} _{1}}{|\mathbf {r} -\mathbf {r} _{1}|^{3}}}\ \cdot \ {\frac {\mathbf {r} -\mathbf {r} _{2}}{|\mathbf {r} -\mathbf {r} _{2}|^{3}}}\ \mathrm {d} ^{3}r}
应用一条矢量恒等式 ,
∇
(
1
|
r
−
r
′
|
)
=
−
(
r
−
r
′
)
|
r
−
r
′
|
3
{\displaystyle \nabla \left({\frac {1}{|\mathbf {r} -\mathbf {r} '|}}\right)=-\ {\frac {(\mathbf {r} -\mathbf {r} ')}{|\mathbf {r} -\mathbf {r} '|^{3}}}}
可以得到
U
i
n
t
=
q
1
q
2
16
π
2
ϵ
0
∫
V
∇
(
1
|
r
−
r
1
|
)
⋅
∇
(
1
|
r
−
r
2
|
)
d
3
r
=
q
1
q
2
16
π
2
ϵ
0
∫
V
∇
⋅
[
1
|
r
−
r
1
|
∇
(
1
|
r
−
r
2
|
)
]
−
(
1
|
r
−
r
1
|
)
∇
2
(
1
|
r
−
r
2
|
)
d
3
r
{\displaystyle {\begin{aligned}U_{int}&={\frac {q_{1}q_{2}}{16\pi ^{2}\epsilon _{0}}}\int _{\mathbb {V} }\nabla \left({\frac {1}{|\mathbf {r} -\mathbf {r} _{1}|}}\right)\ \cdot \ \nabla \left({\frac {1}{|\mathbf {r} -\mathbf {r} _{2}|}}\right)\mathrm {d} ^{3}r\\&={\frac {q_{1}q_{2}}{16\pi ^{2}\epsilon _{0}}}\int _{\mathbb {V} }\nabla \ \cdot \ \left[{\frac {1}{|\mathbf {r} -\mathbf {r} _{1}|}}\nabla \left({\frac {1}{|\mathbf {r} -\mathbf {r} _{2}|}}\right)\right]-\ \left({\frac {1}{|\mathbf {r} -\mathbf {r} _{1}|}}\right)\nabla ^{2}\left({\frac {1}{|\mathbf {r} -\mathbf {r} _{2}|}}\right)\mathrm {d} ^{3}r\\\end{aligned}}}
。 应用散度定理 ,可以将这方程右手边第一个项目,从体积积分变为面积积分:
∫
V
∇
⋅
[
1
|
r
−
r
1
|
∇
(
1
|
r
−
r
2
|
)
]
d
3
r
=
∮
S
[
1
|
r
−
r
1
|
∇
(
1
|
r
−
r
2
|
)
]
⋅
d
2
r
{\displaystyle \int _{\mathbb {V} }\nabla \ \cdot \ \left[{\frac {1}{|\mathbf {r} -\mathbf {r} _{1}|}}\nabla \left({\frac {1}{|\mathbf {r} -\mathbf {r} _{2}|}}\right)\right]\mathrm {d} ^{3}r=\oint _{\mathbb {S} }\left[{\frac {1}{|\mathbf {r} -\mathbf {r} _{1}|}}\nabla \left({\frac {1}{|\mathbf {r} -\mathbf {r} _{2}|}}\right)\right]\cdot \mathrm {d} ^{2}r}
其中,
S
{\displaystyle \mathbb {S} }
V
{\displaystyle \mathbb {V} }
假设
V
{\displaystyle \mathbb {V} }
狄拉克δ函数 的矢量恒等式
∇
2
(
1
|
r
−
r
′
|
)
=
−
4
π
δ
(
r
−
r
′
)
{\displaystyle \nabla ^{2}\left({\frac {1}{|\mathbf {r} -\mathbf {r} '|}}\right)=-4\pi \delta (\mathbf {r} -\mathbf {r} ')}
可以得到
U
i
n
t
=
q
1
q
2
4
π
ϵ
0
∫
A
L
L
S
P
A
C
E
δ
(
r
−
r
2
)
|
r
−
r
1
|
d
3
r
=
1
4
π
ϵ
0
q
1
q
2
|
r
1
−
r
2
|
{\displaystyle U_{int}={\frac {q_{1}q_{2}}{4\pi \epsilon _{0}}}\int _{\mathbb {ALL\ SPACE} }{\frac {\delta (\mathbf {r} -\mathbf {r} _{2})}{|\mathbf {r} -\mathbf {r} _{1}|}}\ \mathrm {d} ^{3}r={\frac {1}{4\pi \epsilon _{0}}}\ {\frac {q_{1}q_{2}}{|\mathbf {r} _{1}-\mathbf {r} _{2}|}}}
这就是双点电荷系统的电势能。














































![{\displaystyle {\begin{aligned}U&={\frac {\epsilon _{0}}{2}}\int _{\mathbb {V} }[\mathbf {\nabla } \cdot \mathbf {E} (\mathbf {r} )]\phi (\mathbf {r} )\ \mathrm {d} ^{3}r\\&={\frac {\epsilon _{0}}{2}}\int _{\mathbb {V} }\mathbf {\nabla } \cdot [\mathbf {E} (\mathbf {r} )\phi (\mathbf {r} )]-\mathbf {E} (\mathbf {r} )\cdot \mathbf {\nabla } \phi (\mathbf {r} )\ \mathrm {d} ^{3}r\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/446c291ef417157fa508e331f011af19e8c81858)
![{\displaystyle U={\frac {\epsilon _{0}}{2}}\oint _{\mathbb {S} }[\mathbf {E} (\mathbf {r} )\phi (\mathbf {r} )]\cdot \mathrm {d} ^{2}r-{\frac {\epsilon _{0}}{2}}\int _{\mathbb {V} }\mathbf {E} (\mathbf {r} )\cdot \mathbf {\nabla } \phi (\mathbf {r} )\ \mathrm {d} ^{3}r}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc40158b75eff38aa3c73c40ed01b059a3615227)






![{\displaystyle U={\frac {\epsilon _{0}}{2}}\int _{\mathbb {ALL\ SPACE} }[E(\mathbf {r} )]^{2}\mathrm {d} ^{3}r}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d27be2fee8cef0b528cde368b8a59469a29d118)

![{\displaystyle u(\mathbf {r} )={\frac {\epsilon _{0}}{2}}[E(\mathbf {r} )]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb65b0408212faadd139ec5dbbbe41aec1935e9e)






![{\displaystyle {\begin{aligned}U_{int}&={\frac {q_{1}q_{2}}{16\pi ^{2}\epsilon _{0}}}\int _{\mathbb {V} }\nabla \left({\frac {1}{|\mathbf {r} -\mathbf {r} _{1}|}}\right)\ \cdot \ \nabla \left({\frac {1}{|\mathbf {r} -\mathbf {r} _{2}|}}\right)\mathrm {d} ^{3}r\\&={\frac {q_{1}q_{2}}{16\pi ^{2}\epsilon _{0}}}\int _{\mathbb {V} }\nabla \ \cdot \ \left[{\frac {1}{|\mathbf {r} -\mathbf {r} _{1}|}}\nabla \left({\frac {1}{|\mathbf {r} -\mathbf {r} _{2}|}}\right)\right]-\ \left({\frac {1}{|\mathbf {r} -\mathbf {r} _{1}|}}\right)\nabla ^{2}\left({\frac {1}{|\mathbf {r} -\mathbf {r} _{2}|}}\right)\mathrm {d} ^{3}r\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b2093a2c677cf8564ad81d271f720a4aa193b95)
![{\displaystyle \int _{\mathbb {V} }\nabla \ \cdot \ \left[{\frac {1}{|\mathbf {r} -\mathbf {r} _{1}|}}\nabla \left({\frac {1}{|\mathbf {r} -\mathbf {r} _{2}|}}\right)\right]\mathrm {d} ^{3}r=\oint _{\mathbb {S} }\left[{\frac {1}{|\mathbf {r} -\mathbf {r} _{1}|}}\nabla \left({\frac {1}{|\mathbf {r} -\mathbf {r} _{2}|}}\right)\right]\cdot \mathrm {d} ^{2}r}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7af2116b42b296be35687226e1731cb70f5fc17)


