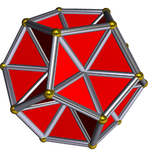
大稀有三角六十面体
 (按这里观看旋转模型) | ||||
| 类别 | 星形多面体 稀有多面体 | |||
|---|---|---|---|---|
| 对偶多面体 | 完全星形二十面体 | |||
| 识别 | ||||
| 名称 | 大稀有三角六十面体 | |||
| 鲍尔斯缩写 | hudsi[1] | |||
| 性质 | ||||
| 面 | 60 | |||
| 边 | 90 | |||
| 顶点 | 20 | |||
| 欧拉特征数 | F=60, E=90, V=20 (χ=-10) | |||
| 边长 | (长边) (短边) | |||
| 组成与布局 | ||||
| 面的种类 | 等腰三角形 | |||
| 顶点图 | 九角星 | |||
| 图像 | ||||
| ||||
大稀有三角六十面体(英语:great noble triangular hexecontahedron[1])是完全星形二十面体的对偶多面体,属于稀有多面体[2],外观为有20个星状尖角的多面体,且面与面有较复杂的交差模式,乔治·奥利舍夫斯基(George Olshevsky)称其为“Huitzilopochtli”,其与完全星形二十面体都具备等面和等角的特性[3]。大稀有三角六十面体是一种星形六十面体,由60个全等的等腰三角形组成,每个顶点都是9个等腰三角形的公共顶点。大稀有三角六十面体的顶点排列方式与正十二面体相同,但顶点间的相连关系与正十二面体不同,因此其可以视为是正十二面体的一种刻面结果。[4][5]
虽然大稀有三角六十面体被视为是正十二面体的一种刻面结果,但其也可以被认为是与星形二十面体对偶性密切相关的立体。对于后者,帕特里克·杜·瓦尔对完整星形二十面体胞之壳层的命名,在《五十九种二十面体》中的星形二十面体集合中依次使用,被称为标准的命名规则。而星形二十面体对偶系列立体缺乏这样的规则,这也是其鲍尔斯缩写依照其对偶多面体来命名的原因。[1]
性质
[编辑]大稀有三角六十面体共由60个面、90条边和20个顶点所组成,其中60个面都是等腰三角形每个顶点都是9个等腰三角形的公共顶点。其90条边中有30条长边和60条短边。
顶点图
[编辑]由于这个立体是完全星形二十面体的对偶多面体,根据对偶多面体的性质,其为面与顶点互换,也就是说,对偶多面体是将原始多面体的顶点变成对偶多面体的面、原始多面体的面变成对偶多面体的顶点,边与新的顶点连接,因此原有多面体的面会成为对偶多面体的顶点图,反之亦然,[6]也就是说大稀有三角六十面体的顶点图会是九角星,对应完全星形二十面体的面。顶点图为九角星意味着顶点周围之面的排列方式会依循九角星边的连接方式:[1]
 组成大稀有三角六十面体 顶点周围面的 排列方式(顶点图,以蓝色表示) |
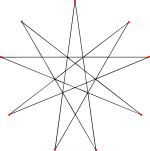 大稀有三角六十面体 的顶点图 |
面的组成
[编辑]大稀有三角六十面体由60个等腰三角形组成,也就是说大稀有三角六十面体的组成面为等腰三角形。这些等腰三角形有着面跟其他的面相交的性质,[4]因此会导致面有部分隐没在图形内部,并非所有部分皆可见,因此难以直接从外观识别出其等腰三角形面。如下图,露在外面的部分已蓝色表示、隐没于形状内部的部分以白色表示,黑线为与其他面的交线。
顶点座标
[编辑]大稀有三角六十面体的顶点座标为:[1]
- 、
和的偶排列。
其中为,是黄金比例。
对偶多面体
[编辑]
大稀有三角六十面体的对偶多面体为完全星形二十面体。[7]完全星形二十面体是星形二十面体的一种[8],其包含了星形二十面体的所有胞,因此被称为“完全的”、“最后的”星形二十面体。
相关几何体
[编辑]正十二面体
[编辑]大稀有三角六十面体是正十二面体的刻面多面体,即把正十二面体的顶点用其他边的排列方式重新连接,而不新增顶点或改变顶点的位置。大稀有三角六十面体将正十二面体的顶点改由三个顶点连成三角形。[1][4]
这意味着正十二面体与大稀有三角六十面体共用相同的顶点布局[1]。
小稀有三角六十面体
[编辑]

作为抽象多面体,大稀有三角六十面体与小稀有三角六十面体(small noble triangular hexecontahedron)拓朴同构。[1]小稀有三角六十面体同样是正十二面体的刻面多面体,但刻面的方式与大稀有三角六十面体不同:构成小稀有三角六十面体的等腰三角形来自于正十二面体顶面的一个顶点和底面的两个顶点。[9]其对偶多面体是稀有九角星二十面体,即由星形二十面体的D胞所构成的星形多面体。[9]

|

|
| 小稀有三角六十面体 的面 (蓝色为露在立体 外部的部分) |
小稀有三角六十面体相对于 正十二面体的刻面[9] 刻面后的面以黄色表示 |
小稀有三角六十面体外观与凹五角锥十二面体非常相似。小稀有三角六十面体在外观上皆为每个面向内凹陷五角锥型的立体,差别仅在凹陷程度不同:小稀有三角六十面体的凹陷程度比凹五角锥十二面体来的浅。
-
小稀有三角六十面体
五角柱七百二十胞体
[编辑]| 五角柱七百二十胞体 | |||||
|---|---|---|---|---|---|
| |||||
| 类型 | 稀有均匀多胞体 | ||||
| 维度 | 4 | ||||
| 识别 | |||||
| 名称 | 五角柱七百二十胞体 | ||||
| 鲍尔斯缩写 | paphacki[10] | ||||
| 性质 | |||||
| 胞 | 720个五角柱 | ||||
| 面 | 1800个正方形 720个正五边形 | ||||
| 边 | 1200 | ||||
| 顶点 | 120 | ||||
| 组成与布局 | |||||
| 顶点图 |  大稀有三角六十面体 | ||||
| 对称性 | |||||
| 对称群 | H4, order 14400 | ||||
| 特性 | |||||
| 等角、 等胞 | |||||
大稀有三角六十面体是五角柱七百二十胞体(pentagon-prismatic heptacosicosachoron)的顶点图。[7][10]五角柱七百二十胞体是边的领导元素同于小星形一百二十胞体(small stellated 120-cell)的四维稀有均匀多胞体。[10]这种几何结构非常复杂,堪称是同类几何结构中最复杂的例子之一。[7]
性质
[编辑]五角柱七百二十胞体由720个胞、2520个面、1200条边和120个顶点所组成。其720个胞皆为五角柱。在其2520个面中,有1800个正方形和720个正五边形。每个顶点都是60个五角柱的公共顶点,对应的顶点图为大稀有三角六十面体。[7][10]
顶点座标
[编辑]五角柱七百二十胞体的顶点座标为:
- 、
- 、
以及的全排列。[10]
参见
[编辑]参考文献
[编辑]- ^ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 Richard Klitzing. hudsi (dual of H-stellation of icosahedron). bendwavy.org. [2021-07-27]. (原始内容存档于2021-07-27).
- ^ Mikloweit, Ulrich; et al. Exploring Noble Polyhedra With the Program Stella4D (PDF). Bridges 2020 Conference Proceedings (Tessellations Publishing). 2020: 257–264 [2024-01-16]. (原始内容存档 (PDF)于2023-10-12).
- ^ Robert Webb. Models by Piotr Pawlikowski. www.software3d.com. [2024-01-16]. (原始内容存档于2024-05-23).
George Olshevsky calls this model "Huitzilopochtli". It is the dual of the final stellation of the icosahedron
- ^ 4.0 4.1 4.2 Inchbald, G. Towards stellating the icosahedron and faceting the dodecahedron. Symmetry: Culture and Science. 2000, 11: 1–4 [2024-01-16]. (原始内容存档于2021-06-08).
- ^ Bridge, NJ. Faceting the dodecahedron. Acta Crystallographica Section A: Crystal Physics, Diffraction, Theoretical and General Crystallography (International Union of Crystallography). 1974, 30 (4): 548–552.
- ^ Weisstein, Eric W. (编). Dual Polyhedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ 7.0 7.1 7.2 7.3 Jonathan Bowers. Category 17: Sishi Regiment. polytope.net. [2021-07-26]. (原始内容存档于2020-08-09).
- ^ Eric W. Weisstein. Echidnahedron. 密歇根州立大学图书馆. 1999-05-25 [2016-09-02]. (原始内容存档于2013-06-22).
- ^ 9.0 9.1 9.2 Richard Klitzing. dudsi (dual of D-stellation of icosahedron). bendwavy.org. [2024-01-12]. (原始内容存档于2024-01-08).
- ^ 10.0 10.1 10.2 10.3 10.4 Richard Klitzing. paphacki (pentagon-prismatic heptacosicosachoron). bendwavy.org. [2021-07-26]. (原始内容存档于2021-07-26).