跳转到内容

拉丁超立方抽样

维基百科，自由的百科全书
图中II为拉丁超立方抽样的示意图。I和III则分别为随机抽样与正交抽样的示意图。

拉丁超立方抽样（英語：Latin hypercube sampling，缩写LHS）是一种从多元参数分布中近似随机抽样的方法，属于分层抽样技术，常用于计算机实验或蒙特卡洛积分等。

麦凯（McKay）等人于1979年提出了拉丁超立方抽样。[1]不过此前Eglājs于1977年独立提出过相同的抽样技术。[2]1981年，伊曼（Ronald L. Iman）等进一步发展了该方法。[3]

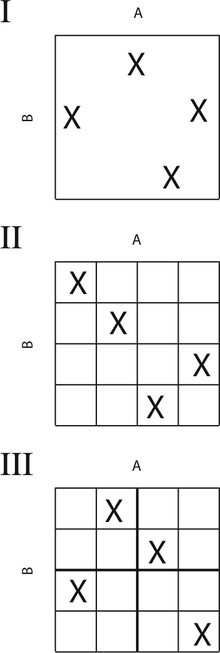
在统计抽样中，拉丁方阵是指每行、每列仅包含一个样本的方阵。拉丁超立方则是拉丁方阵在多维中的推广，每个与轴垂直的超平面最多含有一个样本。

假设有个变量（维度），可以将每个变量分为个概率相同的区间。此时，可以选取个满足拉丁超立方条件的样本点。需要注意的是，拉丁超立方抽样要求每个变量的分区数量相同。不过，该方法并不要求当变量增加时样本数同样增加。

参考文献

[编辑]
  1. ^ McKay, M.D.; Beckman, R.J.; Conover, W.J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code (JSTOR Abstract). Technometrics (American Statistical Association). May 1979, 21 (2): 239–245. ISSN 0040-1706. JSTOR 1268522. OSTI 5236110. doi:10.2307/1268522. 
  2. ^ Eglajs, V.; Audze P. New approach to the design of multifactor experiments. Problems of Dynamics and Strengths. 35 (Riga: Zinatne Publishing House). 1977: 104–107 （俄语）. 
  3. ^ Iman, R.L.; Helton, J.C.; Campbell, J.E. An approach to sensitivity analysis of computer models, Part 1. Introduction, input variable selection and preliminary variable assessment. Journal of Quality Technology. 1981, 13 (3): 174–183. 

延伸阅读

[编辑]
检索自“https://zh1.bitforum.be.eu.org/w/index.php?title=拉丁超立方抽样&oldid=68705947”